Using computer algorithms to create art used to be something only a small group of artists also skilled in the arcane arts of programming could do. But with the invention of Deep Learning algorithms such as style transfer and Generative Adversarial Networks (GANs - more on these in a bit), and the availability of open source code and pre-trained models, it is quickly becoming an accessible reality for anyone with some creativity and time. As Wired succinctly put it, “We Made Our Own Artificial Intelligence Art, and So Can You”:
“I was soon looking at the yawning blackness of a Linux command line—my new AI art studio. Some hours of Googling, mistyped commands, and muttered curses later, I was cranking out eerie portraits. I may reasonably be considered “good” with computers, but I’m no coder; I flunked out of Codecademy’s easy-on-beginners online JavaScript course. And though I like visual arts, I’ve never shown much aptitude for creating my own. My foray into AI art was built upon a basic familiarity with the command line [and access to pre-existing code and models].”
This level of accessibility becoming the norm was made clearer than ever with the release of BigGan, the latest and greatest in the world of GANs. Soon, all sorts of people who had nothing to do with its creation were playing around with it and spawning strange and wonderful AI creations. And these creations were so esoteric and interesting, that we were inspired to write this article highlighting them.

A Primer on Image Synthesis
Before we dive into the survey of fun BigGan creations, let’s get some necessary technical exposition out of the way (those already aware of these details can freely skip). Image Synthesis refers to the process of creating realistic images from random input data. This is done using generative adversarial networks (GANs), which was introduced in 2014 by Ian Goodfellow et al. GANs mainly consist of two networks: the discriminator and the generator. The discriminator is tasked with deciding whether an input image is real or fake, whereas the generator is given random noise and attempts to generate realistic images from the learnt distribution of the training data.
4 years of GAN progress (source: https://t.co/hlxW3NnTJP ) pic.twitter.com/kmK5zikayV
— Ian Goodfellow (@goodfellow_ian) March 3, 2018
GANs are trained on datasets with hundreds of thousands of images. However, a common problem when working on a huge dataset is the stability of the training process. This problem causes the generated images to be not realistic or contain some artifacts. So, BigGan was introduced to resolve these issues.
The Bigger the Better
In order to capture the fine details of the synthesized images we need to train networks that are big i.e contain a lot of trainable parameters. Mainly, GANs contain a moderate number of trainable parameters i.e 50 - 100 million.
In September 2018 a paper titled "Large Scale GAN Training for High Fidelity Natural Image Synthesis" by Andrew Brock et al. from DeepMind was published. BigGan are a scaled up version of previous approaches by providing larger networks and larger batch size. According to the paper: GANs benefit dramatically from scaling, and we train models with two to four times as many parameters and eight times the batch size compared to prior state of the art.
The largest BigGan model has a whooping 355.7 million parameters. The models are trained on 128 to 512 cores of a Google TPU. It provides a state of the art results for image synthesis with IS of 166.3 and FID of 9.6, improving over the previous best IS of 52.52 and FID of 18.65. FID (the lower the better) and IS (the higher the better) are metrics to quantify the the quality of synthesized images. The results are impressive! Just look for yourself:

BigGan models are conditional GANs, meaning they take the class index as an input to generate images from the same category. Moreover, the authors used a variant of hierarchical latent spaces, where the noise vector is inserted into multiple layers of the generator at different depths. This allows the latent vector to act on features extracted from different levels. In less jargon-y terms it makes it easier for the network to know what to generate. The authors characterized instabilities related to large-scale GANs, and created solutions to decrease the instabilities - we won’t get into the details, except to say the solutions work but also have a high computational cost.
The Latent Space
The latent vector is a a lower dimensional representation of the features of an input image. The space of all latent vectors is called the latent space. The latent vector denoted by the symbol $z$, represents an intermediate feature space in the generator network. A generator network follows the architecture of an autoencoder which contains two networks. The first part, the encoder, encodes the input images into a lower dimensional representation (latent vector) using down-sampling. The second part, called the decoder, reconstructs the shape of the image using upsampling. The size of the latent vector is lower than the size of the input (ie, an image) of the encoder. After training a generator network we could discard the encoder part and use the latent vector to construct the generated images. This is useful because it makes the size of the model smaller.
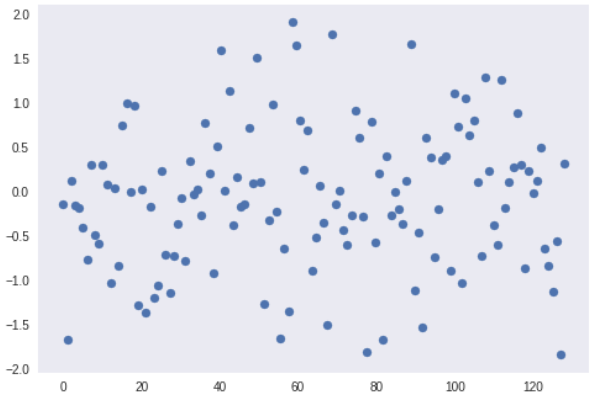
The latent vector has a 1-dimensional shape and is usually sampled from a certain probability distribution, where nearby vectors represent similar generated images. BiGans latent vectors are sampled from a truncated normal distribution. The truncated normal distribution is a normal distribution where the values outside the truncation value are resampled to lie again the region inside the truncation region. Here is a simple graph showing truncated normal distribution in the region $[-2, 2]$:
Reproducible Results Makes for Accessible Art
So, BigGan is a cool model - but why has it been so easy for so many to play with it despite its huge size? In a word: reproducibility.
In order to test any machine learning model first you need an implementation of the model that is simple to import and you need the compute power. The BigGan’s generator network was released for public on TF Hub, a library for reusable machine learning models implemented in TensorFlow. A notebook was also posted on seedbank, a website by Google that collects many notebooks on different fileds of machine learning.
You can open the notebook using google collaboratory, and play around with the model even if you don’t own a GPU; collaboratory offers a kernel with a free GPU for research purposes. The notebook illustrates how to import three BigGan models with different resolutions 128, 256 and 512. Note that each model takes three inputs: the latent vector (a random seed to generate distinctive images), class, and a truncation parameters (which controls the variation of the generated images - see the last section for detailed explanation). Making such models public for artists and researchers has made it easy to create some cool results, without in-depth expertise on the concepts or access to Google-scale resources.
Making Art with BigGan
Since the release of the BigGan’s model by DeepMind, a lot of researchers and artists have been experimenting with it.
Phillip Isola, one of the authors of pix2pix and cycleGans papers, shows how to create a nice 3D effect on BigGan by interpolating between two different poses of a certain class:
March 3, 2018
Mario Klingemann, an artist resident at Google, shows a nice rotary motion in the latent space of BigGan’s by using the sine function:
March 3, 2018
Joel Simon shows how to generate really nice and colorful art by breeding between different classes using GANbreeder:
March 3, 2018
Devin Wilson, an artist, created a simple style transfer effect between different classes of animals by keeping the noise seed and the truncation value the same
March 3, 2018
Gene Kogan, an artist and a programmer, created a mutation of different classes by the means of simple mathematical operations like addition
March 3, 2018
Understanding BigGan’s Latent Space
Let’s dive a bit more into how to create some cool experiments in the latent space. Manipulating the latent vector and truncation values can give us some indications about the distribution of the generated images; in the few last weeks I tried to understand the relations between these variables and generated images. If you want to replicate these experiments you can run this notebook. Let us take a look at some examples.
Breeding
In this experiment we breed between two different classes -- i.e we create intermediate classes using a combination of two different classes. The idea is simple we just average the encoded classes and use the same seed for the latent vector. Given two classes $y_1$ and $y_2$ we use the function
$$\hat{y} = ay_1 + (1-a)y_2$$
Note that using $a = 0.5$ combines the two categories. If $a<0.5$ the generated image will be closer to $y_2$ and if $a>0.5$ it will be similar to $y_1$ .

Background Hallucination
In this experiment we try to change the background of an arbitrary image while keeping the foreground the same. Note that values near zero in the latent vector mainly control the dominant class in the generated image. We can use the $f(x) = \sin(x)$ to resample different background because it preserves values near zero so $\sin(x) \sim x $

Natural zoom
We try to zoom into a certain generated image to observe its fine details. To do that, we need to increase the weights of the latent vector. This doesn't work unless each value in the latent vector has either the value 1 or -1. This can be done by dividing each value in the latent vector by its absolute value namely $\frac{z}{|z|}$. Then we can provide scaling by multiplying by increasing negative values such as $-a \frac{z}{|z|}$

Interpolation
Interpolation refers to the process of finding intermediate data points between specific known data points in the space. The closer the data points the smoother the transition between these points.
The simplest form of an interpolation function is a linear interpolation. Given two vectors $v_1$ and $v_2$ and $N$ as the number of interpolated vectors, we evaluate the interpolation function as
$$F(v_1, v_2, N) = x v_2 + (1-x) v_1 , x \in \left(0,\frac{1}{N}, \cdots, \frac{N}{N}\right)$$
Note that if $x=0$ then the first data point is $v_1$ and if $x=1$ the data point which is the last is $v_2$.
I used interpolations to create a nice zooming effect called “The life of a Beetle ”
The life of a beetle following (5/N) pic.twitter.com/hGvoJvLDMA
— Zaid Alyafeai (زيد اليافعي ) (@zaidalyafeai) November 21, 2018
Truncation Trick
Previous work on GANs samples the latent vector $z \sim \mathcal{N}(0, I)$ as a normal distribution with the identity covariance matrix. On the other hand, the authors of BigGan used a truncated normal distribution in a certain region $[-a, a]$ for $a \in \mathbb{R}^+$ where the sampled values outside that region are resampled to fall in the region. This resulted in better results of both IS and FID scores. The drawback of this is a reduction in the overall variety of vector sampling. Hence there is a trade-off between sample quality and variety for a given network G.
Notice that if $a$ is small then the generated images from a truncated normal distribution will not vary a lot because all the values will be near zero. In the following figure we vary the truncation value from left to right with an increasing value. For each pair we use the same truncation value but we resample a new random vector. We notice that the variation of the generated increases as we increase the truncation value.

Final Thoughts
The availability of reusable models, open source code, and free compute power has made it easy for researchers, artists and programmers to play around with such models and create some cool experiments. When BigGan was introduced on Twitter I had zero knowledge about how it works. But, experimenting with the shared notebook of DeepMind was an incentive for me to try to understand more than what is mentioned in the original paper and share my thought process with the community.
However, we are still far from understanding the hidden world of the latent space. How does the latent vector create the generated image? Can we define more controlled interpolated images by adjusting certain features of the latent vector? Maybe you as a reader will help answering such questions by exploring the available notebooks and trying to implement your own ideas.
Citation
For attribution in academic contexts or books, please cite this work as
Zaid Alyafeai, "BigGanEx: A Dive into the Latent Space of BigGan", The Gradient, 2018.
BibTeX citation:
@article{AlyafeaiGradient2018Gans,
author = {Alyafeai, Zaid}
title = {BigGanEx: A Dive into the Latent Space of BigGan},
journal = {The Gradient},
year = {2018},
howpublished = {\url{https://thegradient.pub/bigganex-a-dive-into-the-latent-space-of-biggan/ } },
}
If you enjoyed this piece and want to hear more, subscribe to the Gradient and follow us on Twitter.