Causation is everywhere in life. Economics, law, medicine, physics, statistics, philosophy, religion, and many other disciplines are inseparable from the analysis of cause and effect. However, compared to other concepts such as statistical correlation, causality is very difficult to define. Using intuition, we can easily judge the causal relationship in daily life; however, it is often beyond the ability of ordinary people to accurately answer the question “What is causality?” in clear, unambiguous language.
Answering this question is so difficult that some philosophers argue that causality is an irreducible, fundamental cognitive axiom that cannot be described any other way. In this article, we describe statistical approaches to developing causal models, which serve as one counterargument to this view.
What is causality
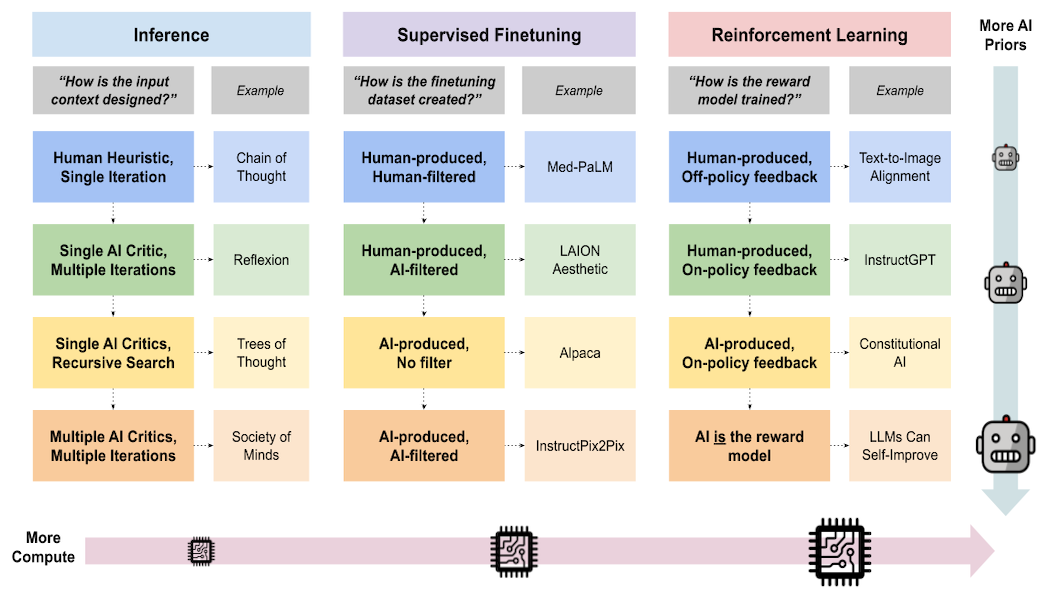
Though there is the epistemological discussion of causality, such as how we might respond to Hume's inductive problem (Hume argues that we cannot make a causal inference by purely a priori means), in this article, we explore statistical approaches to defining what causality is. For example, there are different positions that can be taken on the question of what kind of study might constitute a “cursory overview” or reasonable form of causation (the respective authors use different terms or flavors of “causality”) in the field of information systems (IS). Figure 1 summarizes insights from the MIS Quarterly (a premier IS journal, ranked top 1 in IS) Knowledge Sharing Session on Causality in Quantitative IS Research.
The significance of examining causality is reflected in at least three aspects.
1) It can contribute to a better understanding of the treatment. The term “treatment effect” refers to the causal effect of a binary (0–1) variable on an outcome variable of scientific or policy interest. In the social sciences, the relationship between cause and effect is often murky: the logical chain is often long, and causes can often be latent (hidden). Examining why and how the causal effect exists gives us more reason to believe that the observed causal effect is not a statistical accident and is not a “Type I error.” Empirically confirming the inner workings of this process will lead to a better understanding of the genesis of the outcomes.
2) Once a causal model of how this treatment affects outcomes through specific channels is established, it becomes easier to judge whether the findings can be generalized. If x1 and x2 are correlated and especially if x1 can potentially provoke a change in x2, x2 can be a (causal) channel through which a change in x1 affects y.
3) If we are concerned with human intervention, better understanding the causal relationships could help improve decision-making.
Basic strategies for causal identification
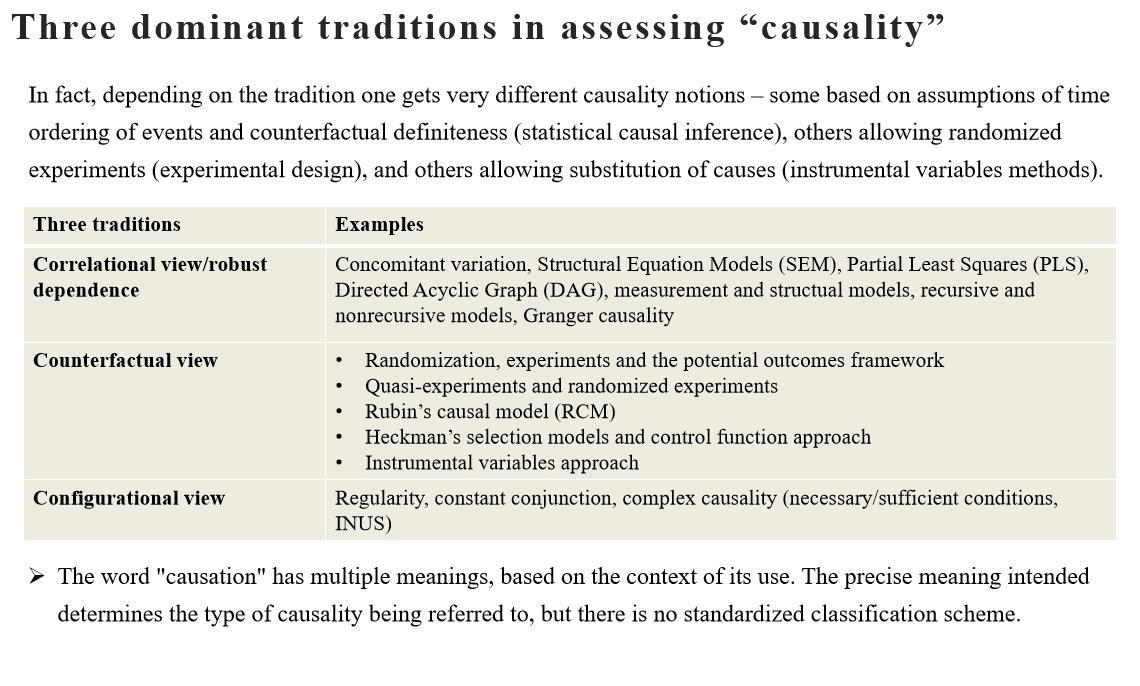
Empirical research on causal inference in quantitative social science is devoted to identifying, estimating, testing, and evaluating causal relationships between socioeconomic phenomena; this is called causal identification and involves the construction of directed graphs to represent these causal relationships. If Y represents the outcome, response, or explained variable, and D represents the cause, treatment, or core explanatory variable being investigated. The causal relationship of interest can be characterized by the basic causal model I in Figure 2.
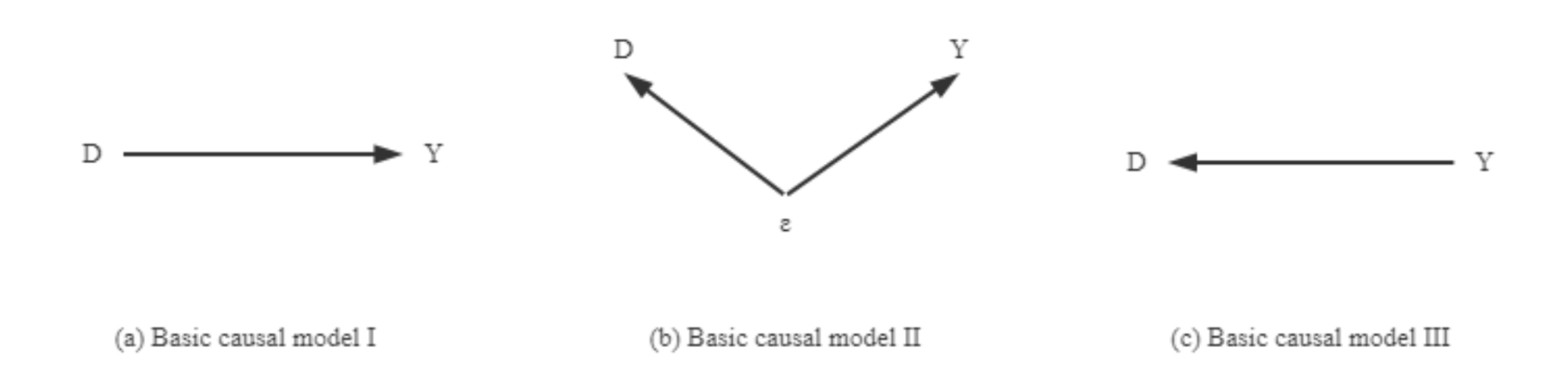
If a causal relationship from D to Y really exists, then there must be a correlation between D and Y, but not vice versa. Several basic causal models may rationalize the fact that D and Y are related: in addition to the basic causal model I, basic causal model II suggests that this correlation may be due to the existence of a third-party confounding factor affecting both D and Y.
Basic causal model III suggests that this correlation may be due to the reverse causality (backward causation) on D. If, in a specific situation, certain assumptions are satisfied between variables, so that a specific causal model has no competing, observationally equivalent causal model. This particular causal model is said to be identified, and such a hypothesis is called an identification hypothesis.
Any causal inference problem consists of two parts: causal identification and statistical inference. For causal identification, what is asked is: if the entire population is available, can population causality be determined? This is the task of social science theory. The basic logic of causal identification is: if correlation does not exist, causality does not exist; if a correlation exists and there is only one causal model that can rationalize this correlation, then this specific causality exists. For statistical inference, the question is: How to obtain information about population causality from sample data? This is the task of statistics. Statistical inference seeks to find the correlation of D and Y in a sample and thereby assess their overall correlation.
There are two basic strategies for causal identification. The first strategy is to look for a specific research context. Different causal identification methods rely on different identification assumptions, and different situations require different identification assumptions. However, sometimes it is difficult to convincingly argue the validity of the identification hypothesis. At this point, the researcher will try the second basic identification strategy - mining the richer, verifiable correlation implications of the causal model (Testable Implications). That is, asking the question: If the causal relationship from D to Y really exists, then what phenomenon will be observed? Different causal models may give different predictions for new correlations, thereby achieving the purpose of validating the model with data by breaking its observational equivalence.
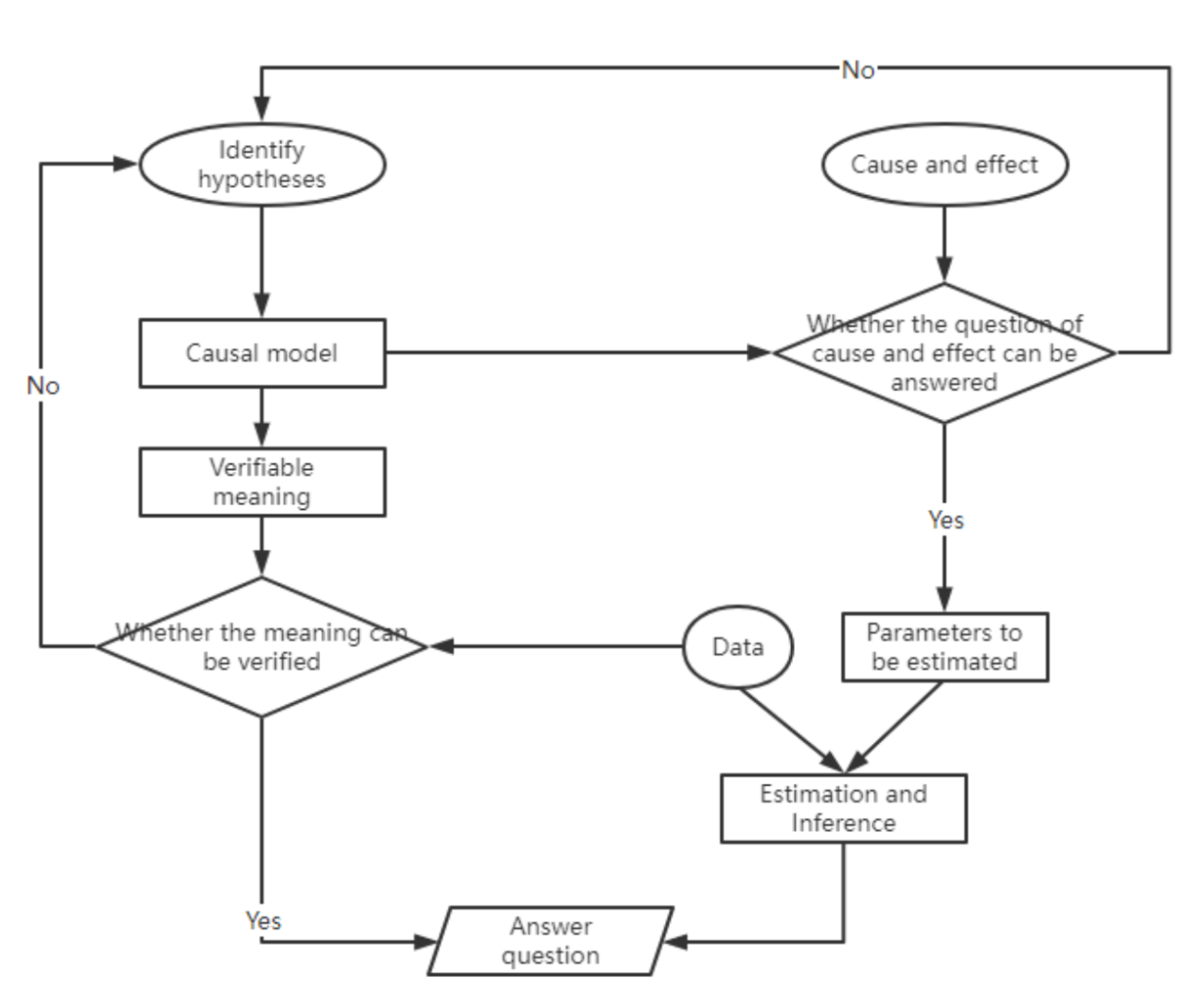
The above two basic identification strategies can be summarized in the process shown in Figure 3. A complete causal inference process consists of three inputs: a causal question, identifying hypotheses, and data. Different research situations correspond to different identification assumptions, thus corresponding to different causal models and causal identification methods. If the model and method under a specific situation and hypothesis can answer the causal question, the parameters to be estimated are proposed, and the data is estimated and inferred to answer the question; if the causal question cannot be answered, consider changing the research context. This is the first basic identification strategy. From the causal model, a new verifiable meaning related to the causal question can be deduced. If this meaning is verified, it indirectly answers the causal question; if it is not verified, consider changing the research context. This is the second basic identification strategy.
Causal inference theory
Causal inference is a theory that describes, discriminates, and measures causal relationships, developed from statistics. For a long time, the development of causal theory in statistics has been very slow due to the lack of a mathematical language to describe causality. It was not until the causal model was proposed at the end of the 20th century that related research began to flourish, providing important data analysis methods for the natural sciences and social sciences. The same theory also makes it possible to apply causal-related techniques and concepts in machine learning. Turing Award winner Judea Pearl called this development process the “causal revolution” and listed seven benefits that the causal revolution could bring to machine learning (Pearl, 2018):
- Encoding Causal Assumptions– Transparency and Testability
- Do-calculus and the control of confounding
- The Algorithmization of Counterfactuals
- Mediation Analysis and the Assessment of Direct and Indirect Effects
- External Validity and Sample Selection Bias
- Missing Data
- Causal Discovery
Judea Pearl’s research on causal inference laid the foundation for current machine learning and robotics technology, and with his book (Pearl, 2009) he brought these ideas to the attention of computer scientists and statisticians.
The commonly used statistical causal models all adopt the interpretation of interventionism: the definition of causality depends on the concept of “intervention”; external intervention is the cause, and the change that produces the phenomenon is the effect.
Pearl proposed that a ‘Mini Turing Test’ is a necessary condition for true intelligence (how quickly a machine can access necessary information, answer questions correctly, and output causal knowledge). By testing the machine learning (ML) models that could capture causal relationships will be more generalizable. Figure 2 summarizes the levels of causality based on Judea Pearl’s work (Pearl & Mackenzie, 2018). The development of more causality in Machine Learning is a necessary step in building more human-like machine intelligence (possibly Artificial General Intelligence).

To address issues in causal inference from observational data, researchers have developed various frameworks, including the potential outcome framework (also known as the Neiman-Rubin potential outcome or Rubin causal model (RCM)) and the structural causal model (SCM).
In recent years, on the basis of the two theoretical frameworks mentioned above (RCM & SCM), the vigorous development of the field of machine learning has promoted the development of the field of causal inference. Employing powerful machine learning methods such as decision trees, ensemble methods, deep neural networks, etc., can more accurately estimate potential outcomes. In addition to improvements in outcome estimation models, machine learning methods also offer a new direction for dealing with confounding problems. Drawing on deep representation learning methods such as generative adversarial neural networks in recent years, the confocal variables are adjusted by learning balanced representations of all covariates, so that the processing task is independent of the confocal variables under the condition of learning representations. In machine learning, the more data, the better. However, in causal inference, simply having more data is not enough. Having more data will only help to obtain more precise estimates, but in the framework of causal inference, there is no guarantee that these causal estimates are correct and unbiased if traditional machine learning techniques are used.
Causal representation learning
Unlike the traditional causal inference approach, which uses causal graphs to connect random variables to complete the causal discovery and reasoning hypothesis task, the problem of causal representation learning has recently attracted more attention. Causal representation learning refers to learning variables from data, which means that machine learning algorithms based on causal representation learning may be able to surpass traditional symbolic AI. It does not require prior knowledge of human partitioning to learn information from data. Directly defining objects or variables related to a causal model is equivalent to directly extracting a more detailed, coarse-grained model of the real world. Although the variables used by every causal model in economics, medicine, or psychology are abstractions of the underlying concepts, it is still very difficult to describe a causal model using coarse-grained variables in the presence of interventions.
The main goal of representation learning in modern machine learning is to learn data representations that retain relevant statistical properties. However, this approach does not take into account the causal nature of the variables; that is, it does not care about the interventional nature of the variables it analyzes or reconstructs. Using representation learning to achieve the purpose of causal learning, the commonality is how to achieve the feature separation (disentanglement) of physical causality in the representation in the physical world and limited data collection. This is especially difficult when data is limited, and the experiment cannot be replicated (i.e., counterfactual). To address this issue, some studies employ generative models or similar ideas to “virtualize” an independent cause in the latent space, while others focus on using attention mechanisms to simulate the prediction process.
Generative models in machine learning can be viewed as a composite of independent mechanisms or “causal” modules (independent causal mechanisms, ICM). The concept of independence has two aspects: one related to influence and one related to information. In the history of causal research, immutable, autonomous, and independent mechanisms have emerged in many forms. For example, Hoover (2006) introduces the true causal order is invariance under appropriate intervention; Aldrich(1989) explores the historical development of these ideas in economics; Pearl(2009) explains autonomy in detail, which holds that causal mechanisms can remain unchanged when other mechanisms are subject to external influences.
We will discuss the attention mechanism in the following section. In general, the introduction of causality will be able to take representation learning to a higher level: moving beyond representations of statistically dependent structures towards models that support intervention, planning, and reasoning, implementing Konrad Lorenz’s concept of thinking as acting in an imagined space.
We can naturally think of incorporating the benefits of causal inference into machine learning, but the reality is not so easy. Causal models often deal with structured data, and cannot deal with high-dimensional, low-level raw data that is common in machine learning, such as images.
To this end, let's go back to the original question: causal representation can be understood as a representation that can be used in a causal model, and causal representation learning is the transformation of raw data such as images into structured variables that can be used in a causal model. Causal representation learning is the bridge connecting causal science and machine learning. Solving this and related problems can well combine causal inference with machine learning to build the next generation of more powerful AI.
Learning modular structures
One direction of causal representation learning is to extract modular structures, i.e., different components of the world exist in a range of environments, tasks, and settings. Then for a model to use the corresponding modules is to take advantage of effective causal representations. For example, suppose changes in natural light (position of the sun, clouds, etc.) mean that the visual environment can be present at several orders of magnitude in brightness. In that case, vision processing algorithms in the human nervous system should employ methods that can factor these changes, rather than building separate face recognizers, say, for various lighting conditions. If the brain compensates for changes in lighting through a gain control mechanism, then the mechanism itself need not have anything to do with the physical mechanisms that cause the difference in brightness. In this direction, Goyal et al. (2019) attempt to embed a set of dynamic modules into a recurrent neural network, coordinated by a so-called attention mechanism, which allows the learning modules to operate independently and dynamically, while also interacting with each other.
Attention mechanism
According to psychological research, the ability of the brain to process complex entities in parallel is limited, and many brain systems representing visual information allocate resources based on competition (running in parallel across the entire visual field). The effect of feedback from high brain regions is known in cognitive science as biased competition. Content-based soft-attention mechanisms operate on typed sets of interchangeable objects. This idea is currently widely used in the state-of-the-art transformer multi-head self-attention model and has achieved good results in many tasks.
Counterfactual
Another interesting research direction in causal representation learning is the application of counterfactual reasoning to domain adaptation problems. The most basic assumption in statistical learning theory is that the training and test data come from the same distribution. However, in most practical cases, the test data is drawn from a distribution that is only related to, but not identical to, the distribution of the training data. This is also a big challenge in causal inference, where counterfactual distributions will generally differ from factual distributions. Therefore, it is necessary to transform causal inference problems into domain adaptation problems by learning from real data to predict counterfactual outcomes.
Semi-supervised learning
Suppose a latent causal graph is X→Y, and we want to learn the mapping from X→Y. In this case, the causal decomposition is P(X,Y)=P(X)P(Y|X).
According to the ICM principle, P(X) does not contain any information of P(Y|X), which means that semi-supervised learning is invalid; that is, using the extra information of P(X) (data without labels) cannot help us improve the estimate of P(Y|X=x). Therefore, semi-supervised learning can only be used in the opposite (reverse causality) direction.
Unsupervised independence: from statistical principles to causal principles
The classic concept of disentangled representation assumes individual latent variables as “sparse encodings of real-world transformations.” Although the concept of so-called “real-world transformation” is difficult to visualize, this insight agnostic to statistical concepts drives supervised approaches to discrete representations. In this approach, relevant transitions can be explicitly identified and manipulated with appropriate datasets and training procedures. In contrast, unsupervised independent representation learning requires learning this real-world transformation from unlabeled data.
Another difficulty that existing machine learning faces is valid training data. For each task/domain, especially in the case of medicine, only limited data is available. In order to improve the effectiveness of the model, it is necessary to find effective ways to search, aggregate, reuse or manually compile the data. This is in stark contrast to the current industry practice of large-scale labeling by humans. Therefore, causal representation learning is a challenge for both human and machine intelligence, but it fits the overall goal of modern machine learning, which is to learn meaningful representations of data, where meaningful representations are robust, transferable, interpretable, or fair.
Future research
In the information age, we are fortunate to have experienced the vigorous data-centric big data revolution (involving machine learning, deep learning, and its applications, such as Alpha-Go, GPT-3, autonomous driving, etc.), which has profoundly changed our lives in every way. The causal relationships in the phenomena of human social and economic life are often intertwined and intricate. When the causal relationship from a specific cause to a specific result is initially verified by the data, researchers will further pay attention to the channel and mechanism of the causal relationship. The starting point of analyzing the channels of causality is that the causal relationship between phenomena may contain multiple logical links, and the cause does not directly act on the result.
Another relatively less well-known, but equally important, causal revolution is underway today, centered on causal science and sweeping across fields, especially artificial intelligence. Although deep learning has greatly advanced the development of machine learning in the past decade, there are still many problems to be solved, such as the ability to transfer knowledge to new problems. Many key problems can be attributed to the OOD (out-of-distribution) problem. Because statistical learning models require an independent and identically distributed (i.i.d.) assumption, statistical learning models tend to make mistakes if the test data and training data come from different distributions. However, in many cases, the assumption of i.i.d. is not valid, and causal inference studies exactly such a situation: how to learn a causal model that can work under different distributions, imply a causal mechanism (Causal Model), and use the causal model for intervention or counterfactual inference.
Essentially, i.i.d. pattern recognition is just a mathematical abstraction, and causality may be essential for most forms of animate learning. However, until now, machine learning has ignored the full integration of causality, and we believe that machine learning will benefit from integrating causal concepts. The researchers believe that combining current deep learning methods with causal tools and ideas may be the only way to go toward general AI systems (Schölkopf et al., 2021).
References
Aldrich, J. (1989). Autonomy. Oxford Economic Papers, 41(1), 15-34.
Goyal, A., Lamb, A., Hoffmann, J., Sodhani, S., Levine, S., Bengio, Y., & Schölkopf, B. (2019). Recurrent independent mechanisms. arXiv preprint arXiv:1909.10893.
Hoover, K. D. (2006). Causality in economics and econometrics.
Pearl, J. (2009). Causal inference in statistics: An overview. Statistics surveys, 3, 96-146.
Pearl, J. (2018). Theoretical impediments to machine learning with seven sparks from the causal revolution. arXiv preprint arXiv:1801.04016.
Pearl, J., & Mackenzie, D. (2018). The book of why: the new science of cause and effect. Basic books.Schölkopf, B., Locatello, F., Bauer, S., Ke, N. R., Kalchbrenner, N., Goyal, A., & Bengio, Y. (2021). Towards causal representation learning 2021. arXiv preprint arXiv:2102.11107.
Citation
For attribution in academic contexts or books, please cite this work as
Wenwen Ding, "Causal Inference: Connecting Data and Reality", The Gradient, 2022.
BibTeX citation:
@article{ding2022causalinference,
author = {Ding, Wenwen},
title = {Causal Inference: Connecting Data and Reality},
journal = {The Gradient},
year = {2022},
howpublished = {\url{https://thegradient.pub/causal-inference-connecting-data-and-reality},
}