Update: Jurgen Schmidhuber kindly suggested some corrections concerning the early work on intrinsic motivation, subgoal discovery and artificial curiosity since 1990, which I have incorporated and expanded.

Suppose your friend just baked and shared an excellent cake with you, and you would like to know its recipe. It might seem that it should be very easy for your friend to just tell you how to cook the cake — that it should be easy for him to get across the recipe. But this is a subtler task than you might think; how detailed should the instructions be? Does the friend have to explain in detail each of the tiny tasks to be followed?

Probably not.

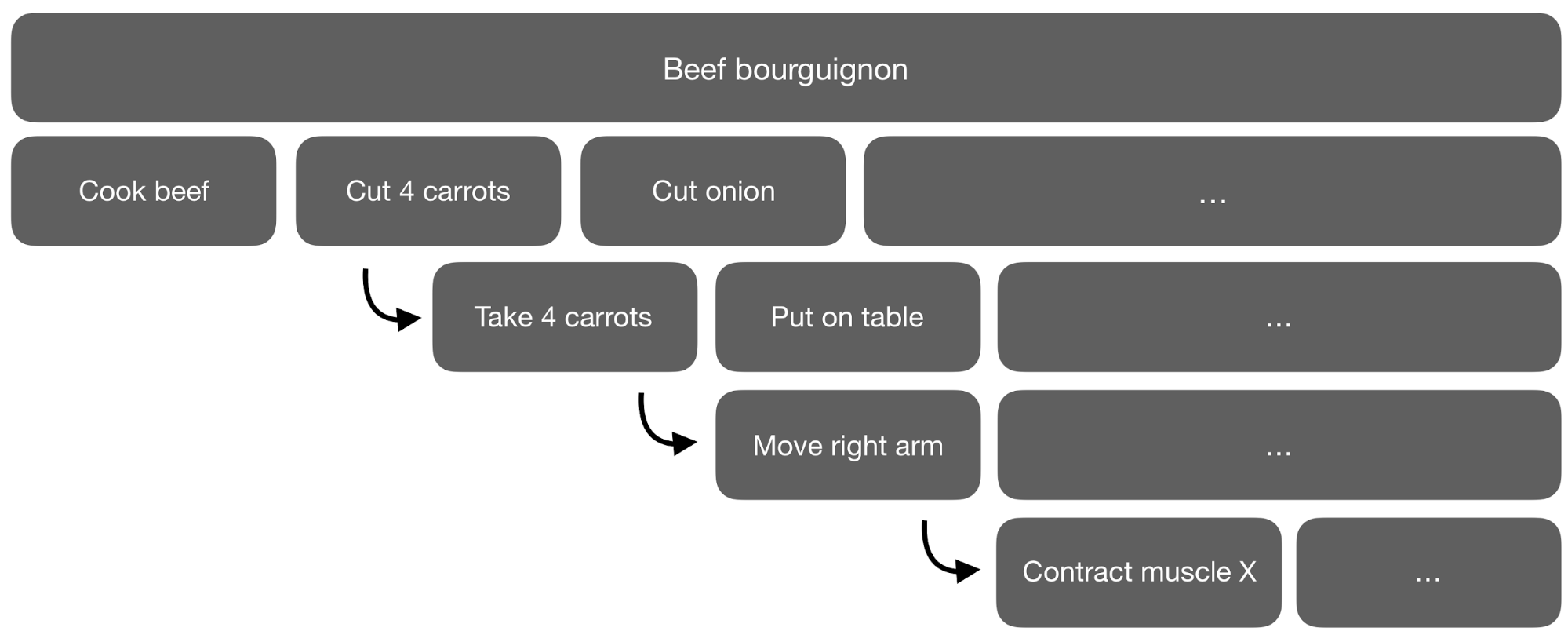
At some point into the recipe of, let's say, beef bourguignon, one needs to "cut 4 carrots into slices." To humans, there is no need to say: "take a knife; in case it doesn't cut properly, sharpen it; take a wooden board and put the 4 carrots on it; hold the knife in your dominant hand; contract muscle X to cut the first slice of carrot."

So, there is a pertinent level of granularity to be adopted when sketching an action for a system to follow. This granularity can be very difficult to mathematically integrate into complex self-learning systems.

In addition, there is converging evidence in developmental psychology ^[1] that newborns, primates, children, and adults rely on the same cognitive systems for their basic knowledge. These cognitive systems include entities, agents, actions, space, social structures and intuitive theories. During open-ended games such as stacking up physically stable block structures, toddlers will use this knowledge to set sub-goals.

To achieve these goals, toddlers seem to generate sub-goals within the space of their basic knowledge, engaging in temporal abstraction. If we use the recipe for beef bourguignon as an example, the cutting process of an onion is a temporally extended action and can take different numbers of steps to complete depending on the required cutting fineness. This idea of temporal abstraction, once incorporated into reinforcement learning (RL), converts it into hierarchical reinforcement learning (HRL).

The following was motivated by a modest attempt to distill research on the subject of HRL. We will start by reviewing the fundamentals of RL before elaborating on its current limitations. We will then see how HRL can be an attractive way to counter the limits of RL, including its motivations, main frameworks and own limitations. Finally, we will discuss active and future research in this area.

---

The If-You-Know-RL-You-Can-Skip-This Section

Reinforcement learning (RL) methods have recently shown a wide range of positive results, including beating humanity's best at Go, learning to play Atari games just from the raw pixels, and teaching computers to control robots in simulations or in the real world. These achievements are the culmination of research on trial and error learning and optimal control since the 1950s. From these two domains was born the field of RL, which has since then been constantly evolving and remains incredibly stimulating.

Csaba Szepesvri puts it well in his book ^[2]: reinforcement learning refers to both a learning problem and a subfield of machine learning.?

In short: the learning problem is concerned with software agents that learn goal-oriented behavior by trial and error in an environment that provides rewards in response to the agent's actions towards achieving that goal.

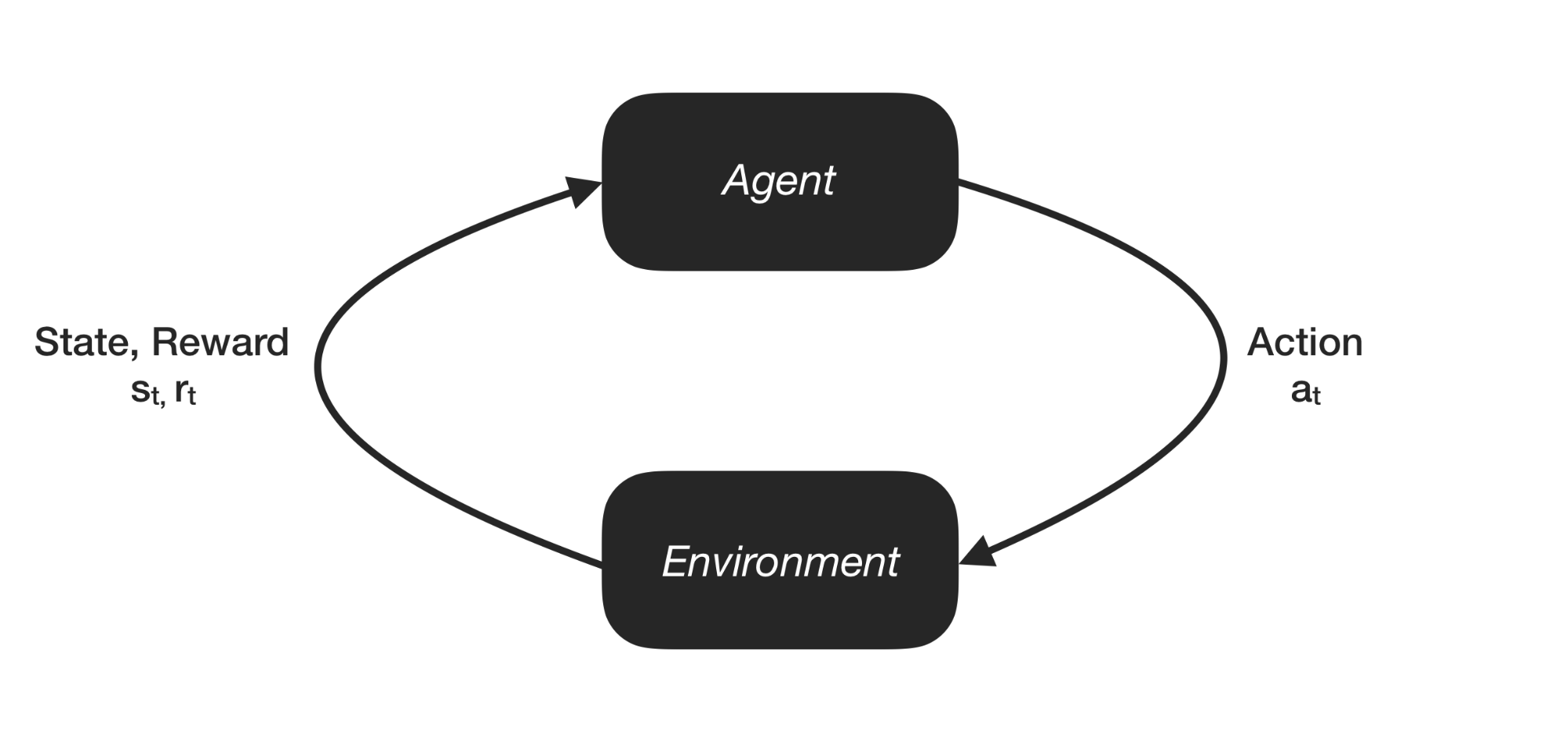
The learning problem setup is quite simple.

There are two protagonists: an agent and an environment. The environment is where the agent lives and what it interacts with. At each point of the interaction, the agent sees an observation of the state of the world, then decides on an action to be taken. The environment changes when the agent acts on it, but it can also change on its own. The agent also receives an environmental reward signal, a number (or a distribution ^[3]) that tells it how good or bad the effect of the action was with respect to the agent?s goal.

At this point, you could ask: why do RL at all and not directly supervised learning (eg. with data samples (state, action) reward)? Alex Graves pointed it in his NeurIPS 2018 talk about Unsupervised Learning:

1. With a supervised learning setup, we would need huge amounts of data that is difficult to obtain and can be complex to define
2. From what we understand from the way toddlers learn when they discover the world ^[4][5][6], learning without relying on a massive amount of data feels more human
3. RL could allow for better generalisation in a variety of complex real-world environments with eg. intrinsic motivation and auxiliary tasks ^{[7][8][9][10]}

The third argument makes even more sense when considering HRL, whose ambition is to be very effective, particularly in terms of generalisation and transfer of learning.

---

Click here for a summary of Markov Decision Processes and RL

Formally speaking, a Markov Decision Processes (MDP) is used to describe an environment for reinforcement learning where the environment is fully observable. Under the well-known Markov property ?the future is independent of the past given the present? we define a finite MDP as a tuple $<S, A, p, r>$ where $S$ is a finite set of states, $A$ is a finite set of actions, $p(s'|s,a)$ is the probability of transition from one state to another $s'$ when action $a$ is taken, $r(s,a,s')$ is a distribution on the rewards obtained when action $a$ is taken from $s$ and the following state $s'$. A stationary deterministic policy $\pi:S\rightarrow A$ maps states to actions.

In short, in a traditional RL problem, the agent aims to maximise its expected discounted return $$R_t = \sum_{k = 0}^\infty \gamma^kr_{t+k+1}$$ where $r_t$ is the reward the agent receives at time $t$ and $\gamma\in[0,1)$ is the discount factor ^[11].

In a fully observable setting, the agent observes the true state of the environment $s_t\in S$ and chooses an action $a_t\in A$ according to policy $\pi(a|s)$.

One way to address the RL problem is to define what is called the action-value function $Q$ of a policy $\pi$ ^[12]: $$Q_{\pi}(s,a) = E[R_{t} | s_{t}=s, a_{t}=a]$$

The Bellman optimality equation $$ Q^\ast (s,a) = r(s,a) + \gamma \sum_{s' \in S} P(s'|s,a) \max_{a'} Q^\ast (s',a') $$

recursively represents the optimal Q-function $$Q^\ast (s,a) = \max_{\pi} Q^{\pi}(s,a)$$ as a function of the expected immediate reward $r(s,a)$ and the transition function $P(s'|s,a)$, which in turn yields an optimal greedy policy $\pi^\ast (s) = \arg\max_{a} Q^\ast (s,a)$.

Q-learning ^[12:1] uses a sample-based approximation of the Bellman optimality equation to iteratively improve the Q-function. Q-learning has been shown to converge in the limit, with probability 1, to the optimal value function
$Q^\ast$ under standard stochastic approximation assumptions. It is a RL solution for a MDP.

In deep Q-learning ^[13], the Q-function is represented by a neural network parameterised by $\theta$.

---

What emerges from the above is really what the main question in RL is: How do we maximize future rewards?

Answering this question actually requires answering to other sub-questions, including:

• What should we learn (models, state utilities, policies, etc.)?
• How should we learn (TD learning, Monte Carlo, etc.)?
• How do we represent what we have learned (deep neural networks, big tables, etc.)?
• How to use what we have learnt: really often the first question that needs to be answered...

---

So, what is hard in RL?

In this famous experiment from Warneken and Tomasello (full video here), an 18-month-old child can understand what is happening and how to interact with the situation without having seen what to do before. The kid must have some common sense to be able to do that: understanding the physics, the action, the constraints, the plan. If you look to the end of the experiment, the child even takes a quick look at the man's hands to deduce how the plan will be completed.

We are still a long way from setting up such a capable system with current RL methods. One reason may be because RL suffers from a variety of defects that hinder learning and prevent it from being applied to more complex environments. HRL aims at alleviating precisely this learning complexity by breaking down specific parts of learning. The question is, therefore, whether this is enough. Strongly in line with Andrey Kurenkov's essay in a previous Gradient article, the main weaknesses of RL, in comparison to the promises of HRL, can be broken down as follows.

• Sample efficiency: data generation is often a bottleneck and current RL methods are data inefficient. With HRL, sub-tasks and abstract actions can be used in different tasks on the same domain (transfer learning)
• Scaling up: the application of classic RL to the problems with large action and/or state space is infeasible (curse of dimensionality). HRL aims to decompose large problems into smaller ones (efficient learning)
• Generalization: trained agents can solve complex tasks, but if we want them to transfer their experience to new (even similar) environments, most state of the art RL algorithms will fail (brittleness due to overspecialization)
• Abstraction: state and temporal abstractions allow to simplify the problem since resulting sub-tasks can effectively be solved by RL approaches (better knowledge representation)

In addition, all the basic algorithms for reinforcement learning are so-called ?flat? methods. They treat the state space as a huge, flat search space, meaning that the paths from the starting state to the target state are very long. If we look at this with the example of the recipe, it would give us a sequence of actions solely composed of a series of muscular micro-contractions. In addition, the length of these paths dictates the cost of learning, as information on future rewards must be disseminated backwards along these paths. In short, the reward signal is weak and delayed.

Perhaps we could step back and look at what we have learnt so far: in the 1970s, research in the field of planning showed that hierarchical methods such as hierarchical task networks ^[14], macro actions ^[15] and state abstraction methods ^[16] can provide exponential reductions in compute costs to find the right plans. There is also a large literature on subgoal discovery, intrinsic motivation and artificial curiosity ^[17][18][19]. Nevertheless, we still lack a fully acceptable method for integrating hierarchies into the effective RL algorithms introduced so far.

---

Hierarchical Reinforcement Learning

As we just saw, the reinforcement learning problem suffers from serious scaling issues. Hierarchical reinforcement learning (HRL) is a computational approach intended to address these issues by learning to operate on different levels of temporal abstraction ^[20].

To really understand the need for a hierarchical structure in the learning algorithm and in order to make the bridge between RL and HRL, we need to remember what we are trying to solve: MDPs. HRL methods learn a policy made up of multiple layers, each of which is responsible for control at a different level of temporal abstraction. Indeed, the key innovation of the HRL is to extend the set of available actions so that the agent can now choose to perform not only elementary actions, but also macro-actions, i.e. sequences of lower-level actions. Hence, with actions that are extended over time, we must take into account the time elapsed between decision-making moments. Luckily, MDP planning and learning algorithms can easily be extended to accommodate HRL.

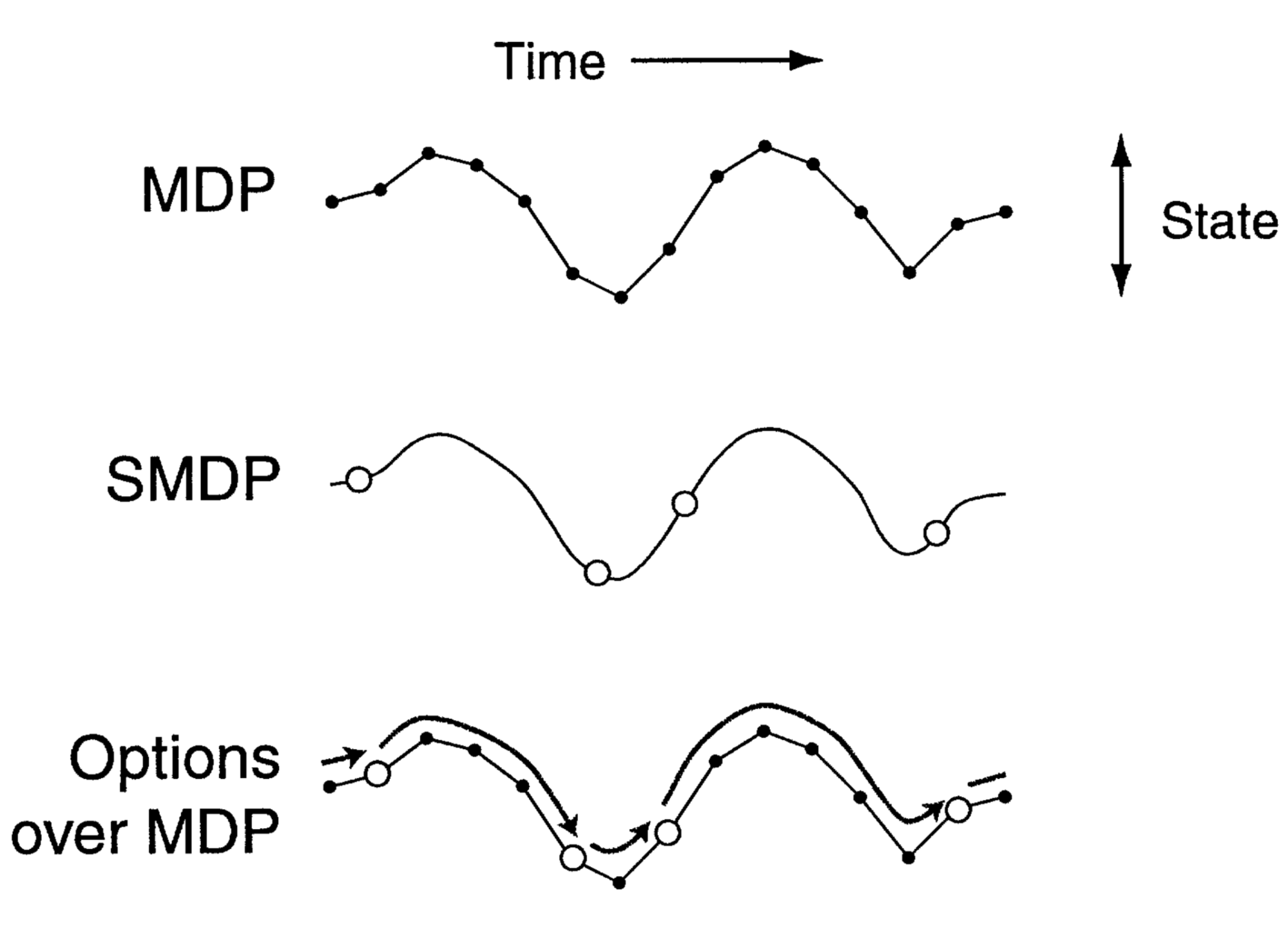
In order to do that, let us welcome the semi-Markov decision process (SMDP). In this setup, $p(s'|s,a)$ turns into $p(s',\tau|s,a)$.

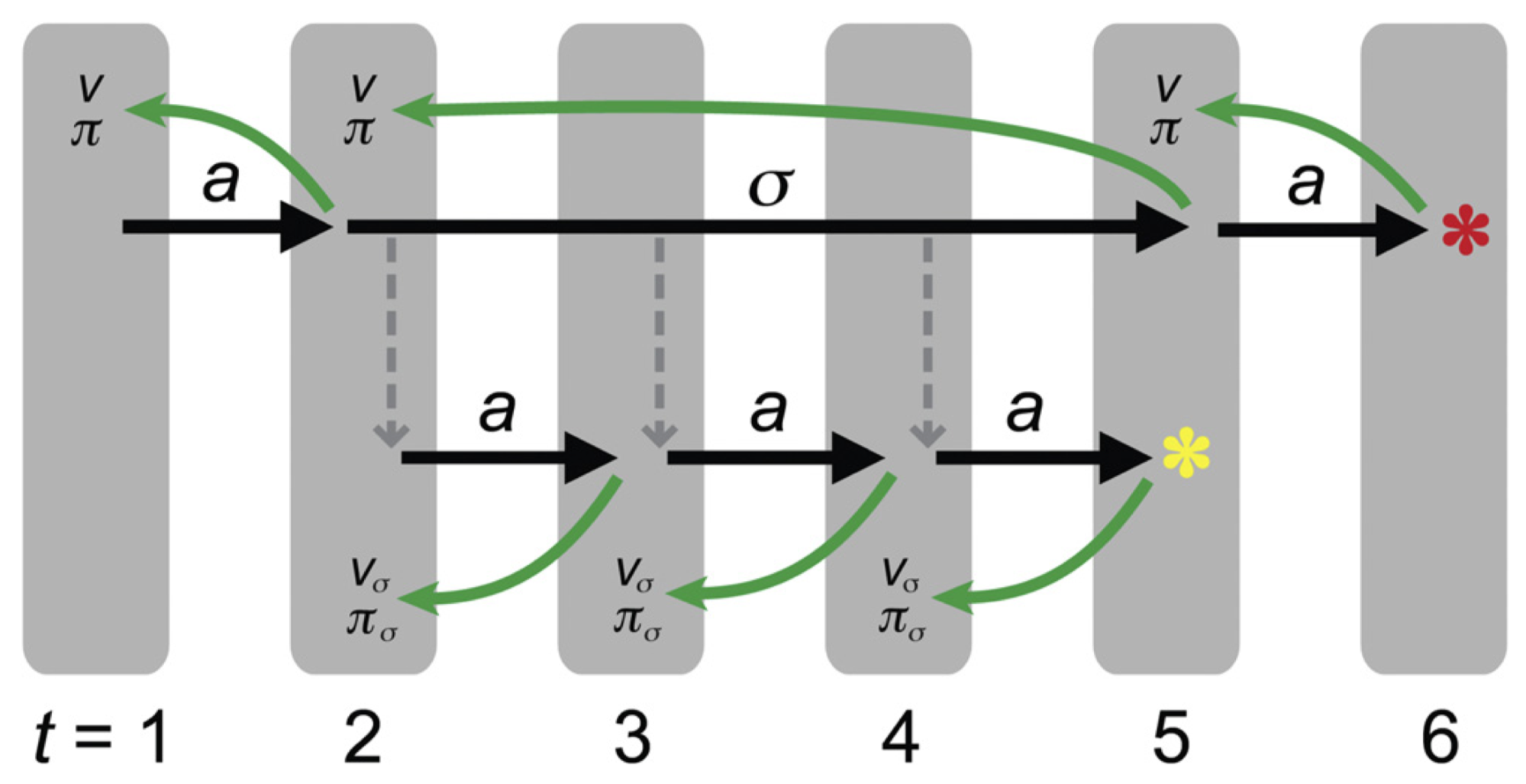
The figure above clearly illustrates the paradigm: $a$ is a primitive action, $\sigma$ is a subroutine or macro-action, $\pi$ is the action policy, $\pi_\sigma$ is the subroutine-specific action polcy, and $V$ and $V_a$ are the state values.

The promise of HRL is to have:

1. Long-term credit assignment: faster learning and better generalisation
2. Structured exploration: explore with sub-policies rather than primitive actions
3. Transfer learning: different levels of hierarchy can encompass different knowledge and allow for better transfer

In the following and in the aforementioned setting, we outline the foundational methods that have emerged since 1993.

---

But, How?

Feudal Learning

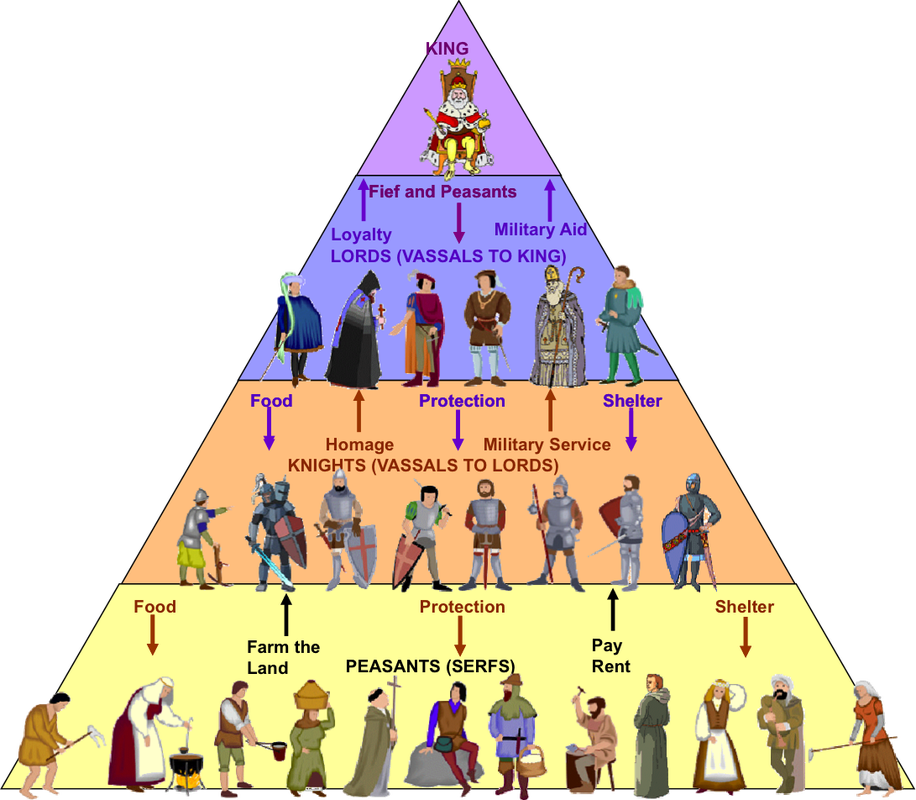
Inspired by Medieval Europe's Feudal system, this HRL method demonstrates how to create a managerial learning hierarchy in which lords (or managers) learn to assign tasks (or sub-goals) to their serfs (or sub-managers) who, in turn, learn to satisfy them. Sub-managers learn to maximize their reinforcement in the context of the command as pictured in the illustration below with the black circle.

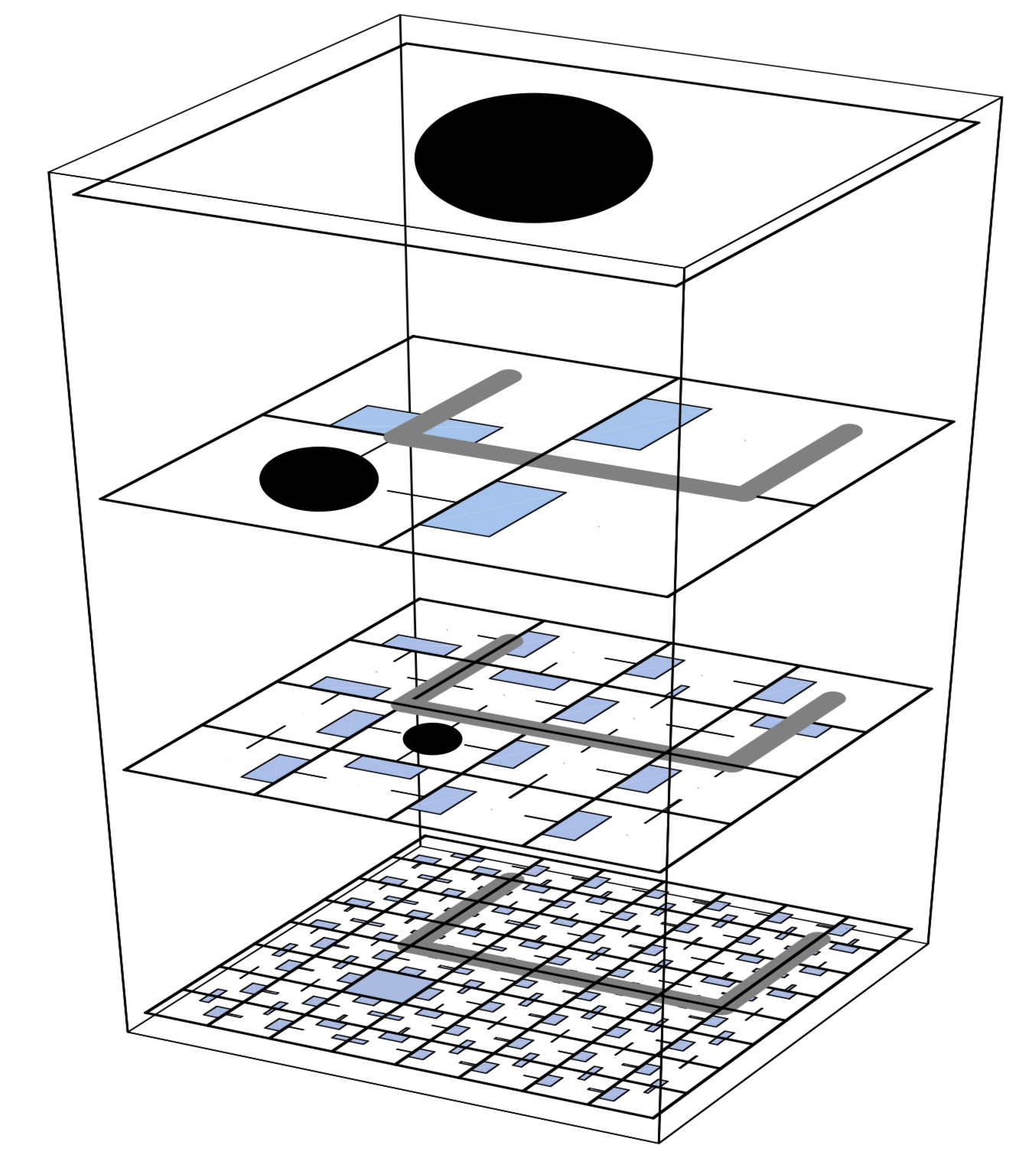
In practice, Feudal learning ^[21] takes advantage of two notions:

• Information hiding: the managerial hierarchy observes the environment at different resolutions
• Reward hiding: communication is made between managers and "workers" through goals - a reward is given for reaching them

A noteworthy effect of information and reward hiding is that the managers only need to know the state of the system at the granularity of their own choices of tasks. They also don?t know what choices their workers have made to satisfy their command, since it is not needed for the system setup to learn.

Unfortunately, the Feudal Q-learning algorithm introduced in ^[21:1] is tailored to a specific kind of problem, and does not converge to any well-defined optimal policy. But it has paved the way for many other contributions.

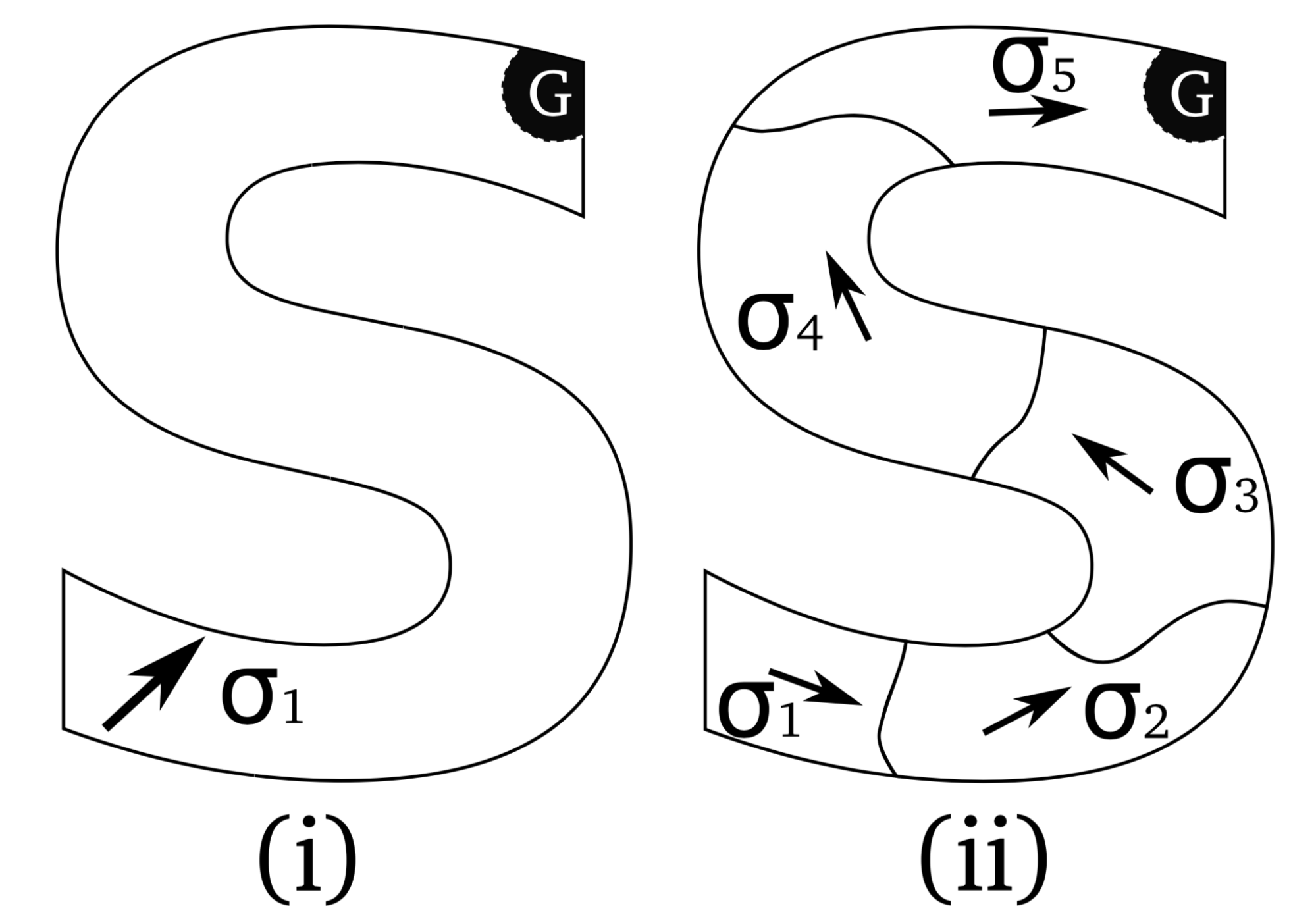
Options Framework

The most well-known formulation for HRL is probably the Options framework ^{[20:1][22][23][24]}. A (Markov) option is a triple $o = <I_o, \pi_o, \beta_o>$ with:

• $I_o$: the initiation set
• $\pi_o: S\times A\rightarrow[0,1]$: the option's policy
• $\beta_o:S\rightarrow[0,1]$: the termination condition

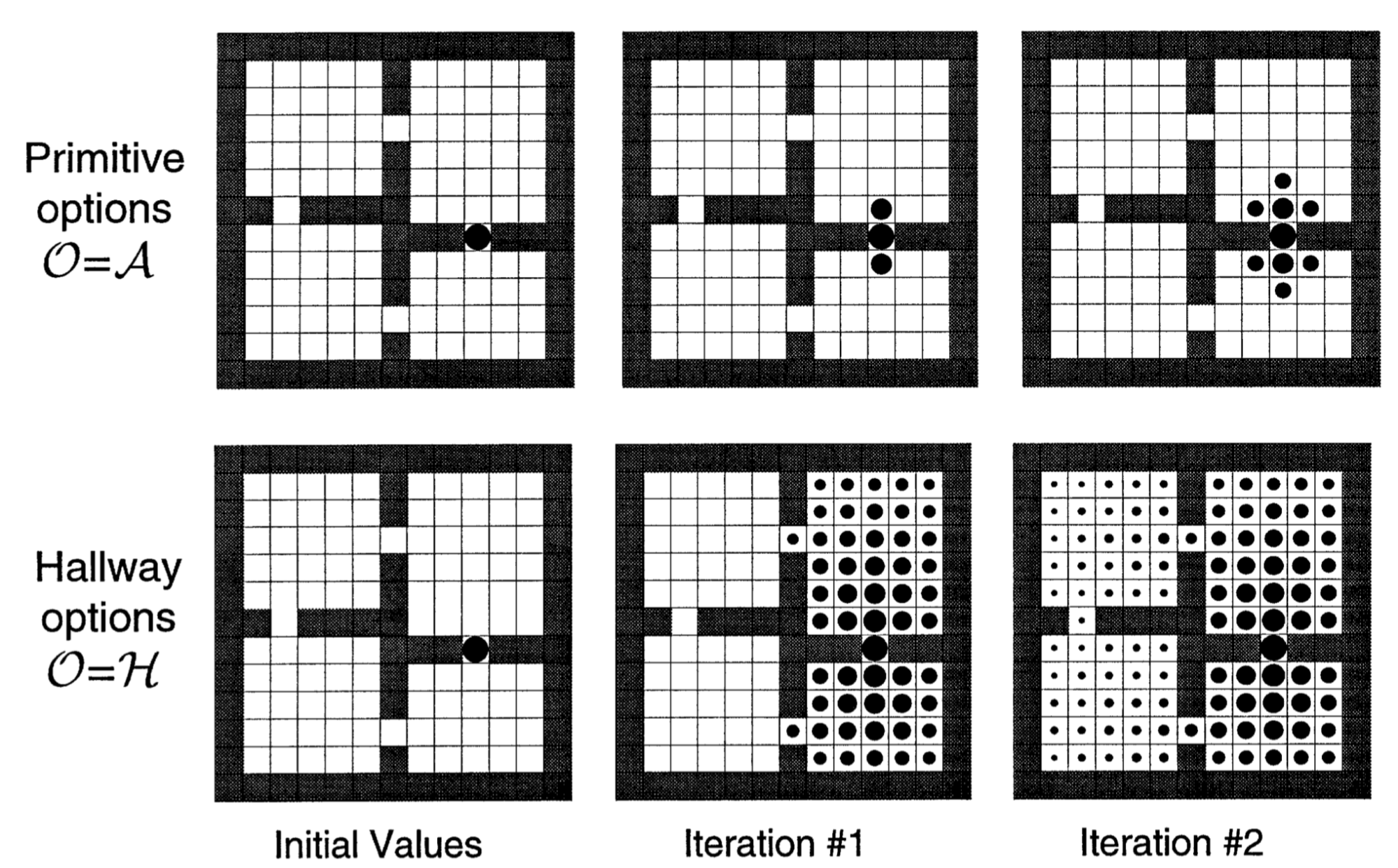
One can grasp the idea of this framework with the self-explanatory example above where the options can be summed up as ?going to hallways? and the actions as ?going N, S, W, or E.? The options can be considered as individual actions at a higher level of abstraction (ie. each state can be used as a subgoal ^[25][26]) and can, as a result, be abstracted into skills.

Unlike Feudal learning, if the action space consists of both primitive actions and options, then an algorithm following the Options framework is proven ^[27] to converge to an optimal policy. Otherwise, it will still converge, but to a hierarchically optimal policy^[28].

The resulting idea is that an Options framework is composed of two levels:

• The bottom level is a sub-policy:
  • takes environment observations
  • outputs actions
  • runs until termination
• The top level is a policy-over-options:
  • takes environment observations
  • outputs sub-policies
  • runs until termination

Options are quite easy to implement, and effective in defining high-level competencies which in turn improves convergence speed. Moreover, options themselves can be used to define option hierarchies. However, and as a natural consequence, options increase the complexity of the MDP. They also do not explicitly address the problem of task segmentation.

Hierarchical Abstract Machines

HAMs consist of non-deterministic finite state machines whose transitions may invoke lower-level machines (the optimal action is yet to be decided or learnt). A machine is a partial policy represented by a Finite State Automaton (FSA). There are four machine states:

• Action states execute an action in the environment
• Call states execute another machine as a subroutine
• Choice states non-deterministically select a next machine state
• Stop states halt execution of the machine and return control to the previous call state

We can view policies as programs. For HAMs, the learning occurs within machines, since machines are only partially defined. The approach is to flatten all machines out and consider the state space of the problem $<s,m>$ where $m$ is the machine state and $s$is the state of the underlying MDP.

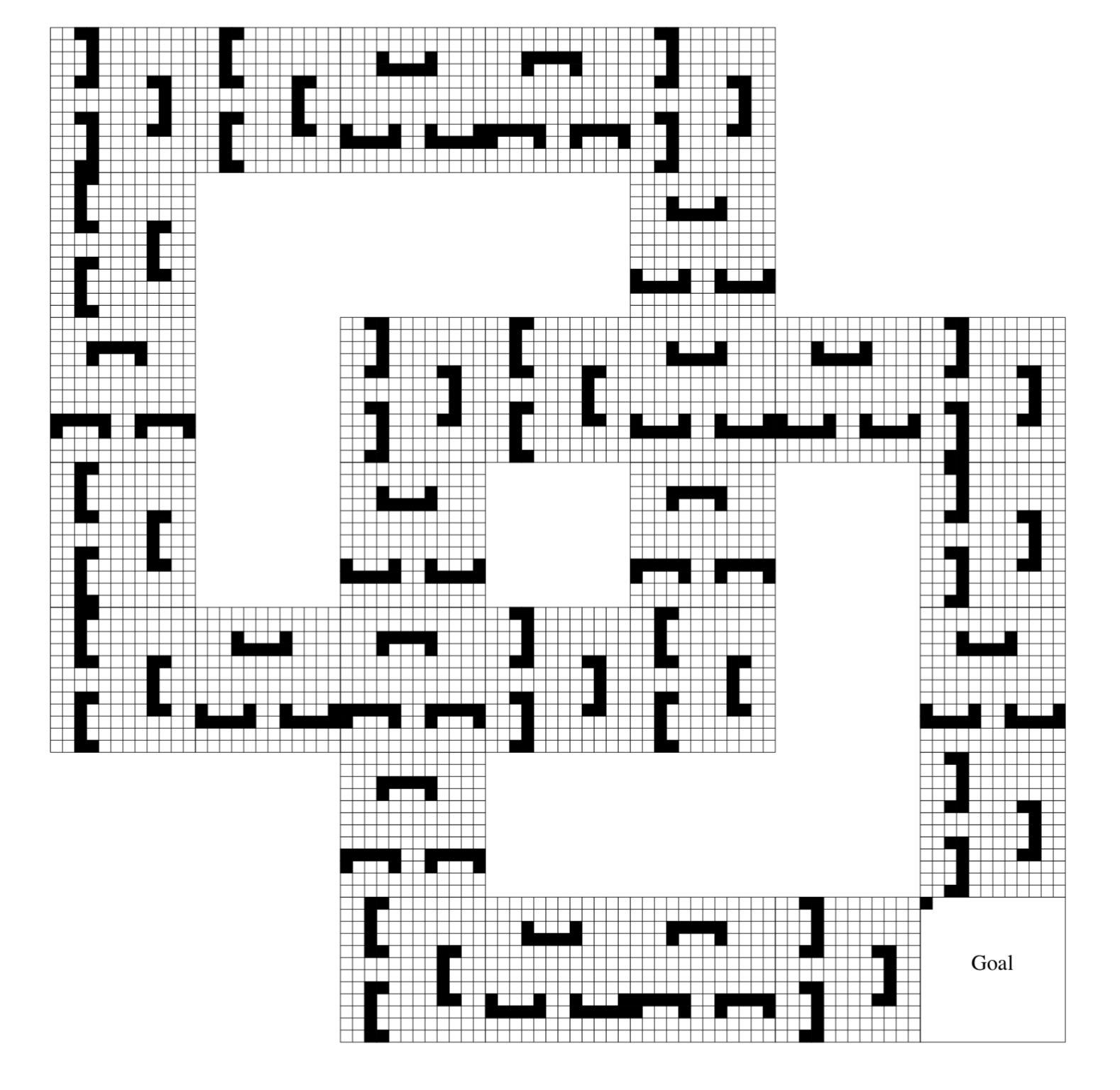
When the machine encounters a Call state, it executes the machine it is supposed to execute in a deterministic way. When it encounters a Stop state, it simply sends the command back to the parent machine. Unlike the case where learning takes place directly on the MDP where actions are learnt in each state, in the HAM framework learning only takes place in the Choice states. Thus, the state space on which the learning takes place may be smaller than the actual state space.

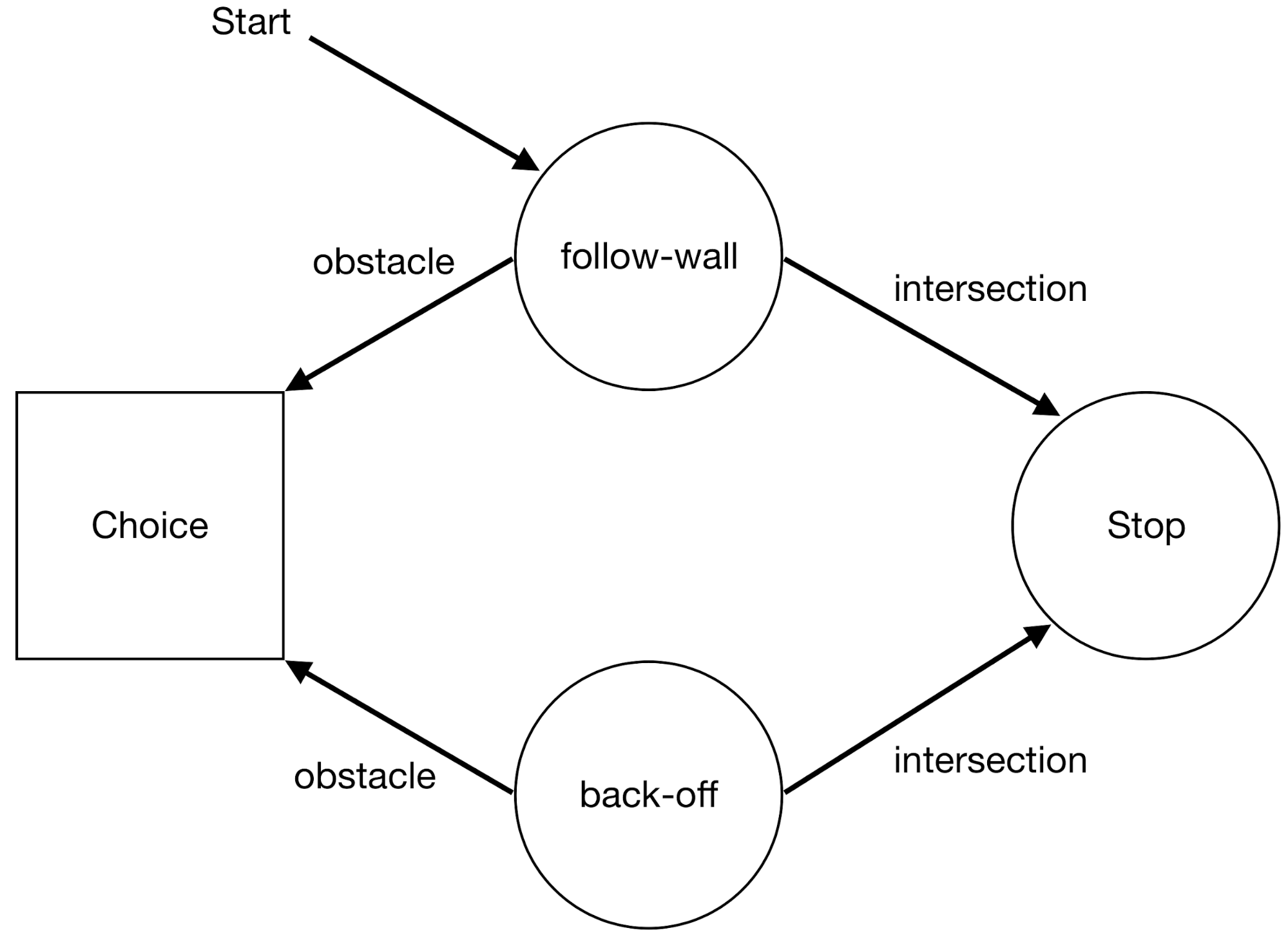
In the above example, each time an obstacle is encountered, the machine enters a Choice state where either it chooses the follow-wall machine (which just continuously follows the wall in a certain direction), or it chooses the back-off machine (which moves back and execution continues).

The learnt machine?s policy is therefore to decide which machine to call and with what probability.

For all the above reasons, the HAM framework offers us the ability to simplify the MDP by restricting the class of realizable policies. Similar to the Options framework, it also has theoretical guarantees of optimality ^[29]. The main problems are that HAMs are complex to design and implement and that there are not many significant applications available.

MAXQ

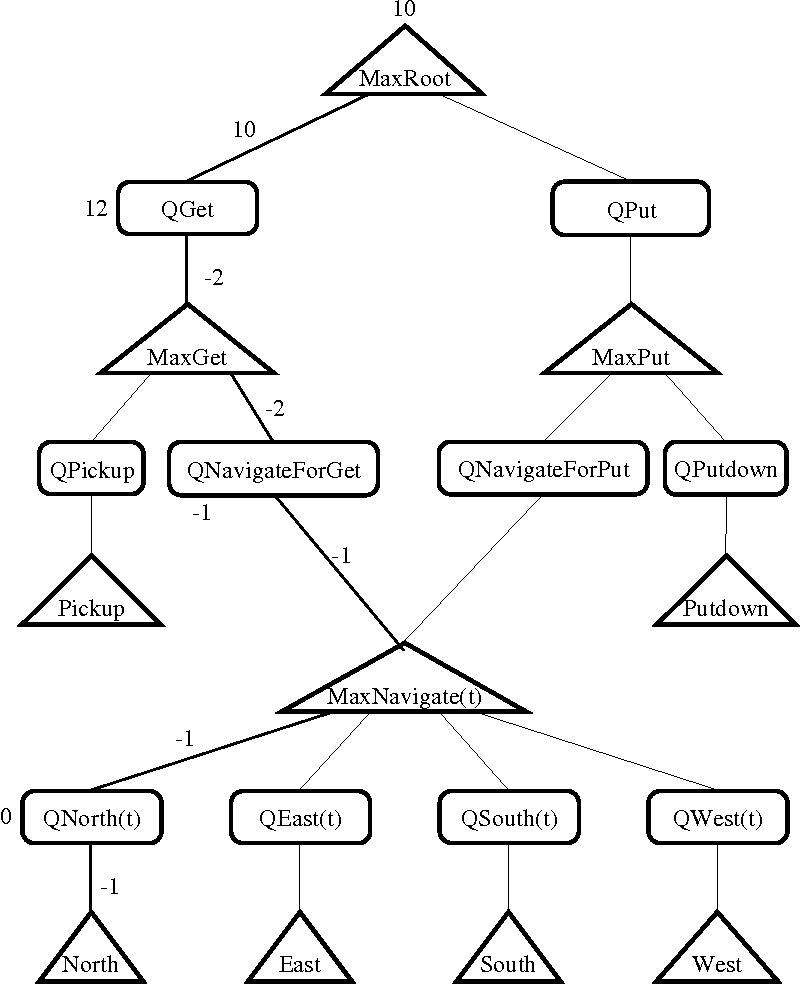
MAXQ is a hierarchical learning algorithm in which the hierarchy of a task is obtained by decomposing the Q value of state-action pair into the sum of two components $Q(p,s,a) = V(a,s) + C(p,s,a)$ where $V(a,s)$ is the total expected reward received when executing the action $a$ in state $s$ (classic $Q$) and $C(p,s,a)$ is the total reward expected from the performance of the parent-task, noted by $p$, after taking the action $a$. In fact, the action $a$ may not only contain a primitive action, but also a sequence of actions.

In essence, one can understand the MAXQ framework ^[30] as decomposing the value function of an MDP into combinations of value functions of smaller constituent MDPs, a finite set of sub-tasks where each sub-task is formalized as 1. a termination predicate, 2. a set of actions and 3. a pseudo reward. For this particular aspect, the MAXQ framework is related to the Feudal Q-learning.

Nevertheless, MAXQ?s advantage over the other frameworks is that it learns a recursively optimal policy, meaning that the policy for a parent task is optimal given the learnt policies of its children. Namely, the task?s policy is context-free: each subtask is optimally solved without reference to the context in which it is executed. While this does not mean it will find an optimal policy, it opens the door to state abstraction and better transfer learning, and can provide common macro actions to many other tasks.

State abstraction helps to reduce memory. Think about it: when you want to reach a door, no matter what colour the door is or whether it is made of wood or metal. State abstraction should help to represent similar states and reject irrelevant state variables. Moreover, with state abstraction, the necessary exploration is reduced and their reusability increased (because they do not depend on their higher parents). In fact, an abstract state is a state with fewer state variables: different states in the world correspond to the same abstract state. Therefore, if we can reduce some state variables (only a few variables are relevant to the task), then we can significantly reduce the learning time. Ultimately, we will use different abstract states for different macro-actions.

In short, the MAXQ framework proposes a real hierarchical decomposition of tasks (contrary to Options), it facilitates the reuse of sub-policies and allows temporal and spatial abstraction. Although one of the concerns is that MAXQ involves a very complex structure and that recursively optimal policies can be highly suboptimal policies.

---

Recent works

Inspired (or interpretable) by these founding elements (Feudal, Options, HAM, MAXQ) of HRL, interesting articles have been published more recently with rather encouraging results.

FeUdal Networks (FUN) for Hierarchical Reinforcement Learning

FeUdal Networks ^[31] present a modular architecture. Inspired by Dayan?s seminal idea of Feudal RL, the manager chooses a direction to go in a latent state space, and the worker learns to achieve that direction through actions in the environment. This means that FuN represents sub-goals as directions in latent state space which then translate into meaningful behavioural primitives. The paper introduces a method that allows better long-term credit assignment and makes memorisation more tractable.

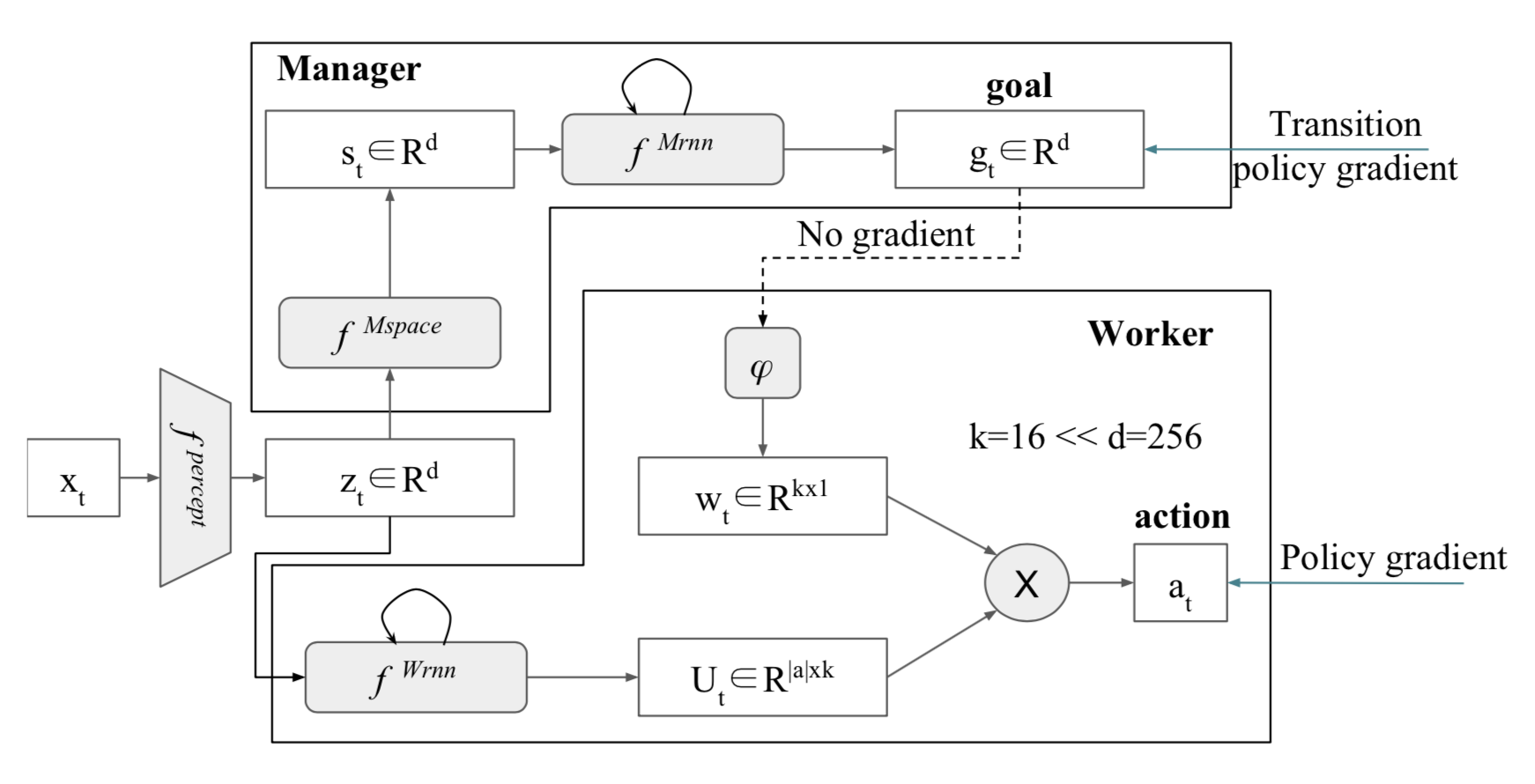
The option-critic architecture

While earlier works used pre-specified option policies, there has been recent success in discovering options such as this paper ^[32] which showcases an end-to-end trainable system that can scale to very large domains with sub-policies with theoretical possibility of learning options jointly with a policy-over-options by extending the policy gradient theorem to options. Contrary to FuN, here the Managers? output is trained with gradients coming directly from the Worker and no intrinsic reward is used.

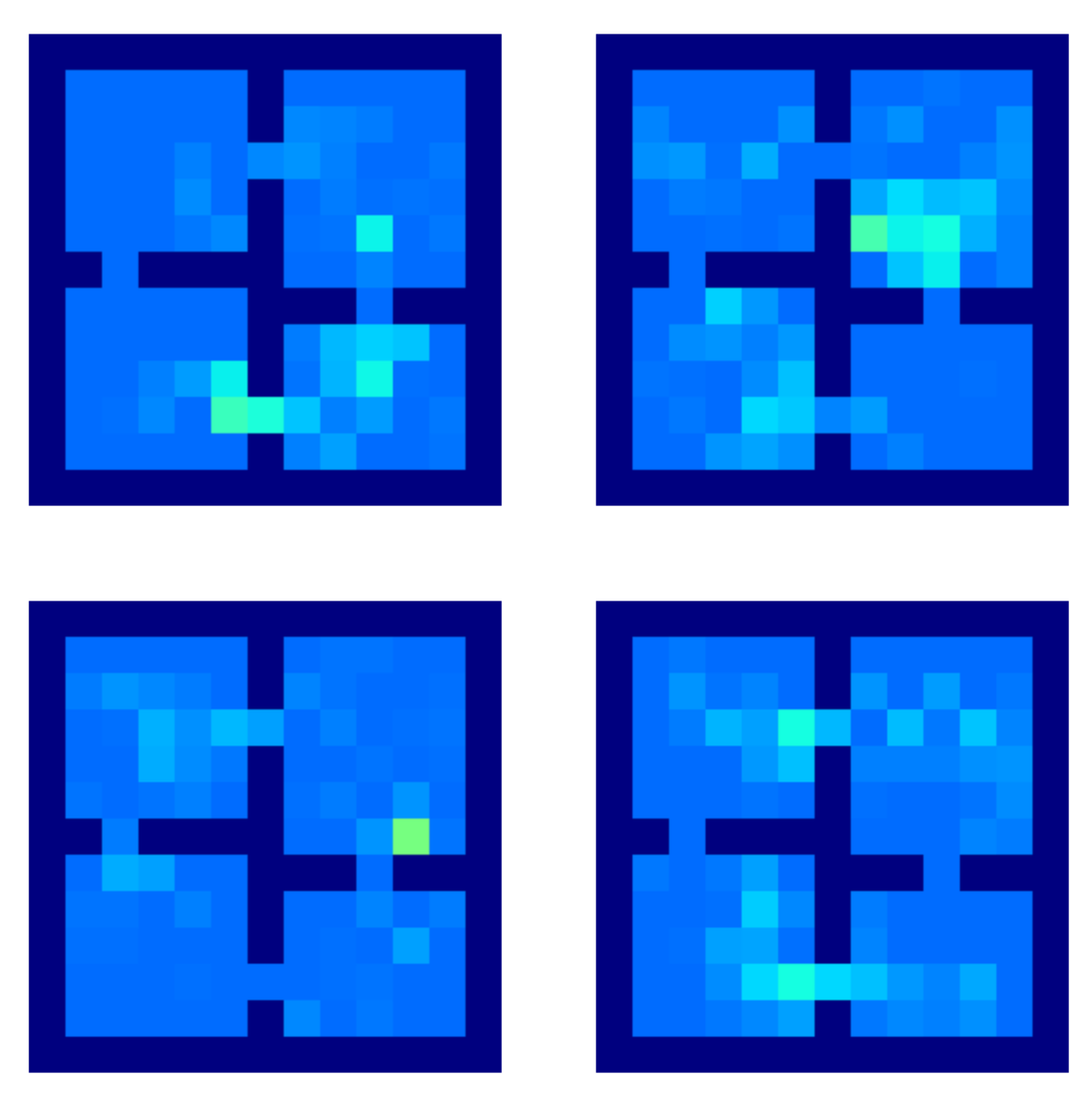
As you can see by the figure above, termination events are more likely to occur near the doors, intuitively this means that reaching those doors are learnt as being meaningful sub-goals.

HIRO (Data Efficient Hierarchical Reinforcement Learning)

The main contribution of ^[33] is that the method is very sample efficient compared to previous works thanks to a novel off-policy correction^[34] and the fact that the learning algorithm directly uses the state observation as the goal. There is no goal representation, hence no goal representation training needed. This means that the higher-level policy receives a meaningful supervision signal from the task reward at the outset.

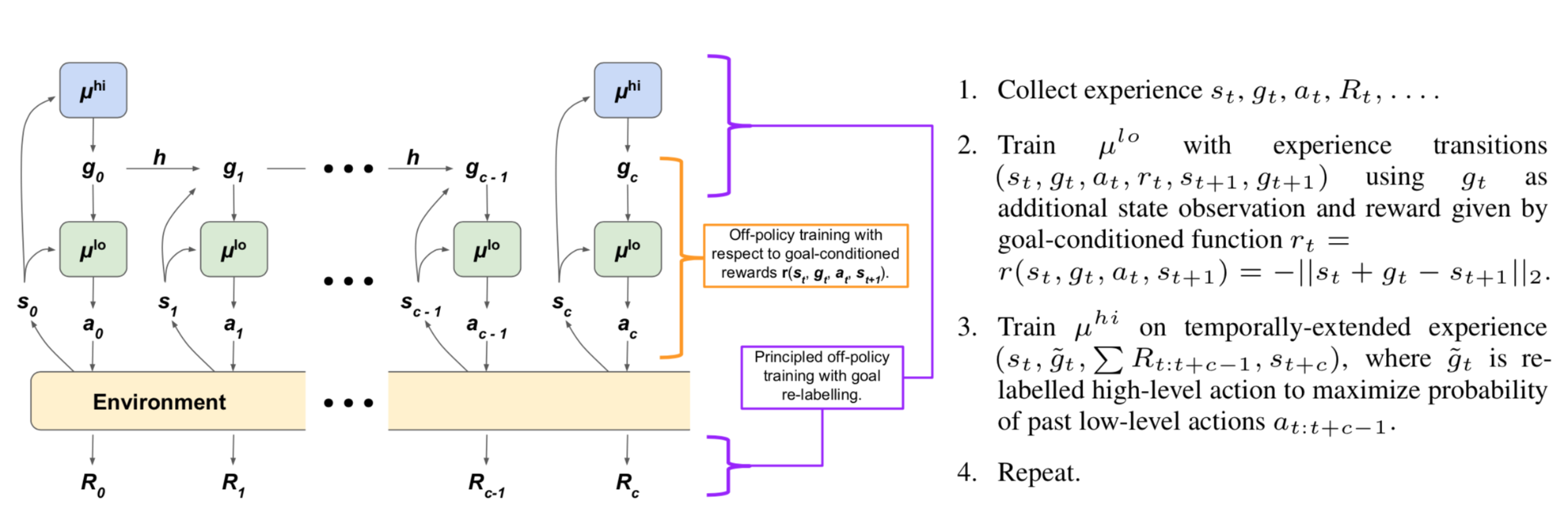
HAC (Learning Multi-Level Hierarchies with Hindsight)

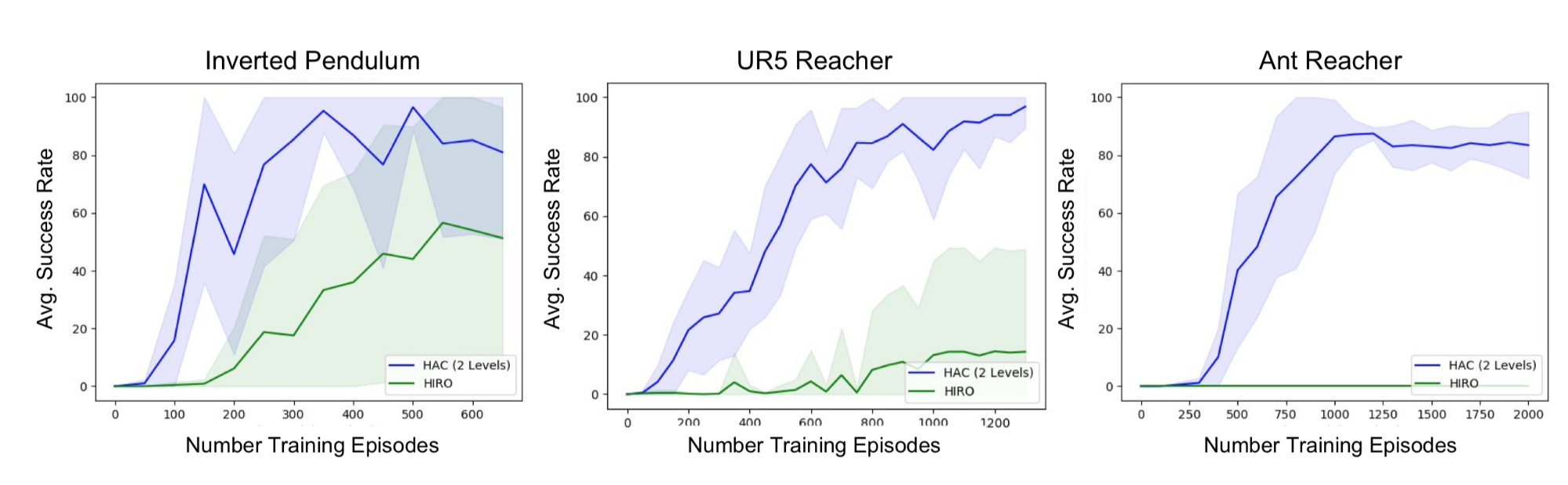
?We introduce a new HRL framework that can significantly accelerate learning by enabling hierarchical agents to jointly learn a hierarchy of policies. Our framework is primarily comprised of two components: (i) a particular hierarchical architecture and (ii) a method for learning the multiple levels of policies in parallel given sparse rewards. The hierarchies produced by our framework have a specific architecture consisting of a set of nested, goal-conditioned policies that use the state space as the mechanism for breaking down a task into subtasks. [...] HIRO, which was developed simultaneously and independently to our approach, uses the same hierarchical architecture, but does not use either form of hindsight and is therefore not as efficient at learning multiple levels of policies in sparse reward tasks.?

Locomotor Controllers

?We study a novel architecture and training procedure for locomotion tasks. A high-frequency, low-level "spinal" network with access to proprioceptive sensors learns sensorimotor primitives by training on simple tasks. This pre-trained module is fixed and connected to a low-frequency, high-level "cortical" network, with access to all sensors, which drives behavior by modulating the inputs to the spinal network. Where a monolithic end-to-end architecture fails completely, learning with a pre-trained spinal module succeeds at multiple high-level tasks, and enables the effective exploration required to learn from sparse rewards.?

This paper introduces a HRL method for training locomotive controllers that effectively improves sample efficiency and achieves transfer among different tasks. The idea of the authors is to obtain low-level policies that are invariable according to the tasks. Then by recycling and re-training the meta-policy that schedules over the low-level policies, different skills can be obtained with fewer samples than by training from scratch.

On Reinforcement Learning for Full-length Game of Starcraft

In this paper, the authors focused on SC2LE, the StarCraft research learning environment introduced by DeepMind. They developed a method for full-length game learning where a controller chooses a sub-policy based on current observations at each relatively large time interval (8 seconds). Then, at each relatively short time interval (one second), a sub-policy chooses a macro-action that is mastered before learning from the repetitions of human expert games. StarCraft is a very challenging playground where the state and action spaces are very large. The approach takes advantage of the hierarchical structure to reduce those spaces. In addition, the size of the execution steps of strategic movements is reduced with the temporal abstraction provided by the controller. Finally, each sub-policy can have its own specific reward function which help divide the complex problem into several easier sub-problems.

h-DQN

?We present hierarchical-DQN (h-DQN), a framework to integrate hierarchical value functions, operating at different temporal scales, with intrinsically motivated deep reinforcement learning. A top-level value function learns a policy over intrinsic goals, and a lower-level function learns a policy over atomic actions to satisfy the given goals. h-DQN allows for flexible goal specifications, such as functions over entities and relations. This provides an efficient space for exploration in complicated environments. We demonstrate the strength of our approach on two problems with very sparse, delayed feedback: (1) a complex discrete stochastic decision process, and (2) the classic ATARI game ?Montezuma's Revenge?.?

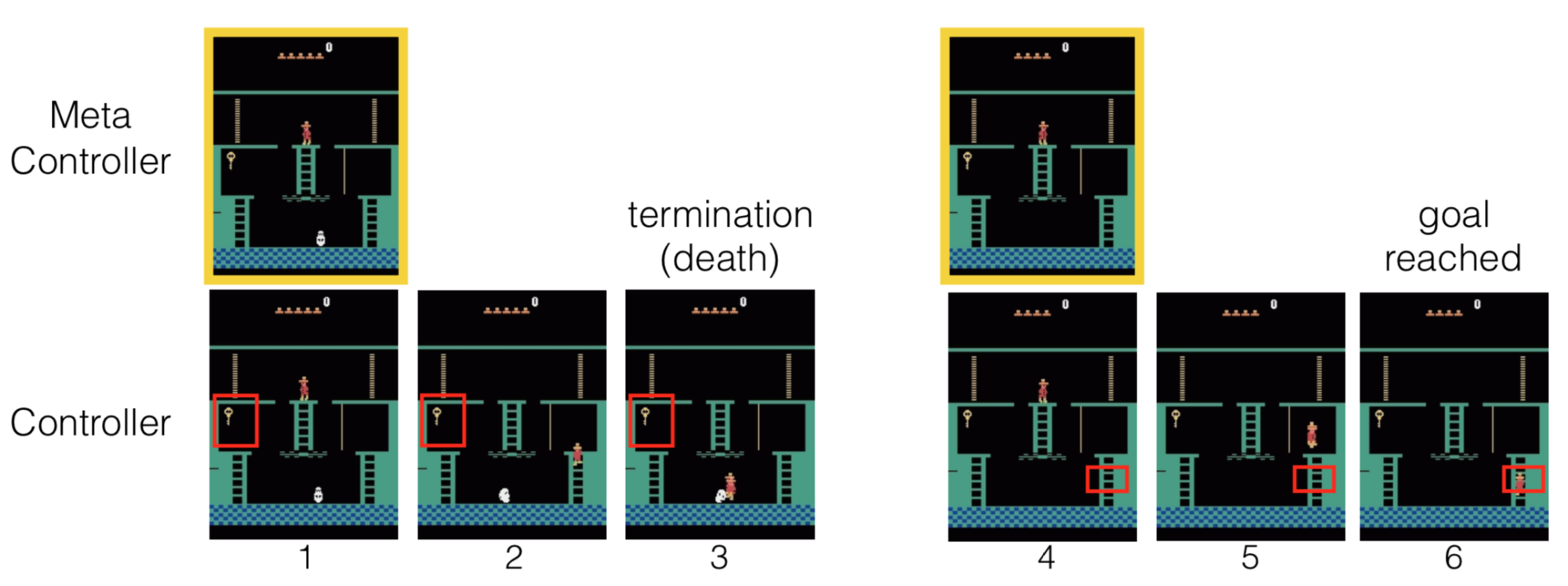
Meta Learning Shared Hierarchies (MLSH)

?In this work, we formulate an approach for the end-to-end meta learning of hierarchical policies. We present a model for representing shared information as a set of sub-policies. We then provide a framework for training these models over distributions of environments. Even though we do not optimize towards the true objective, we achieve significant speedups in learning. In addition, we naturally discover diverse sub-policies without the need for hand engineering.?

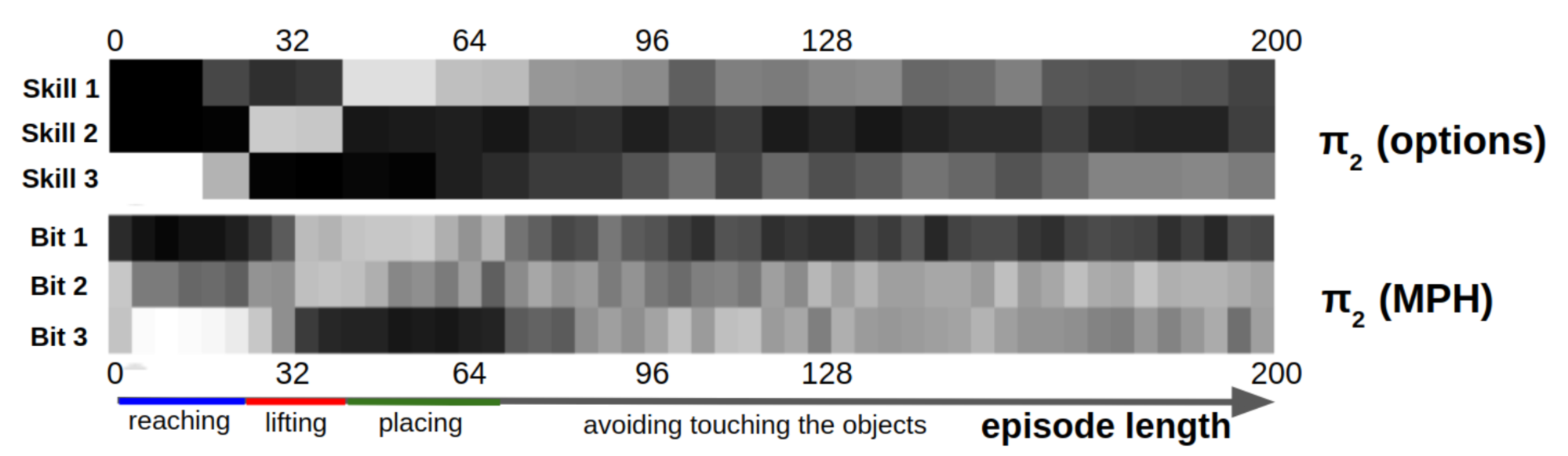
Modulated Policy Hierarchies (MPH)

?We introduced Modulated Policy Hierarchies (MPHs) to address environments with sparse rewards that can be decomposed into sub-tasks. By combining rich modulation signals, temporal abstraction, and intrinsic motivation, MPH benefits from better exploration and increased stability of training. Moreover, in contrast to many state-of-the-art approaches, MPH does not require pre-training, multiple training phases or manual reward shaping. We evaluated MPH on two simulated robot manipulation tasks: pushing and block stacking. In both cases, MPH outperformed baselines and the recently proposed MLSH algorithm, suggesting that our approach may be a fertile direction for further investigation.?

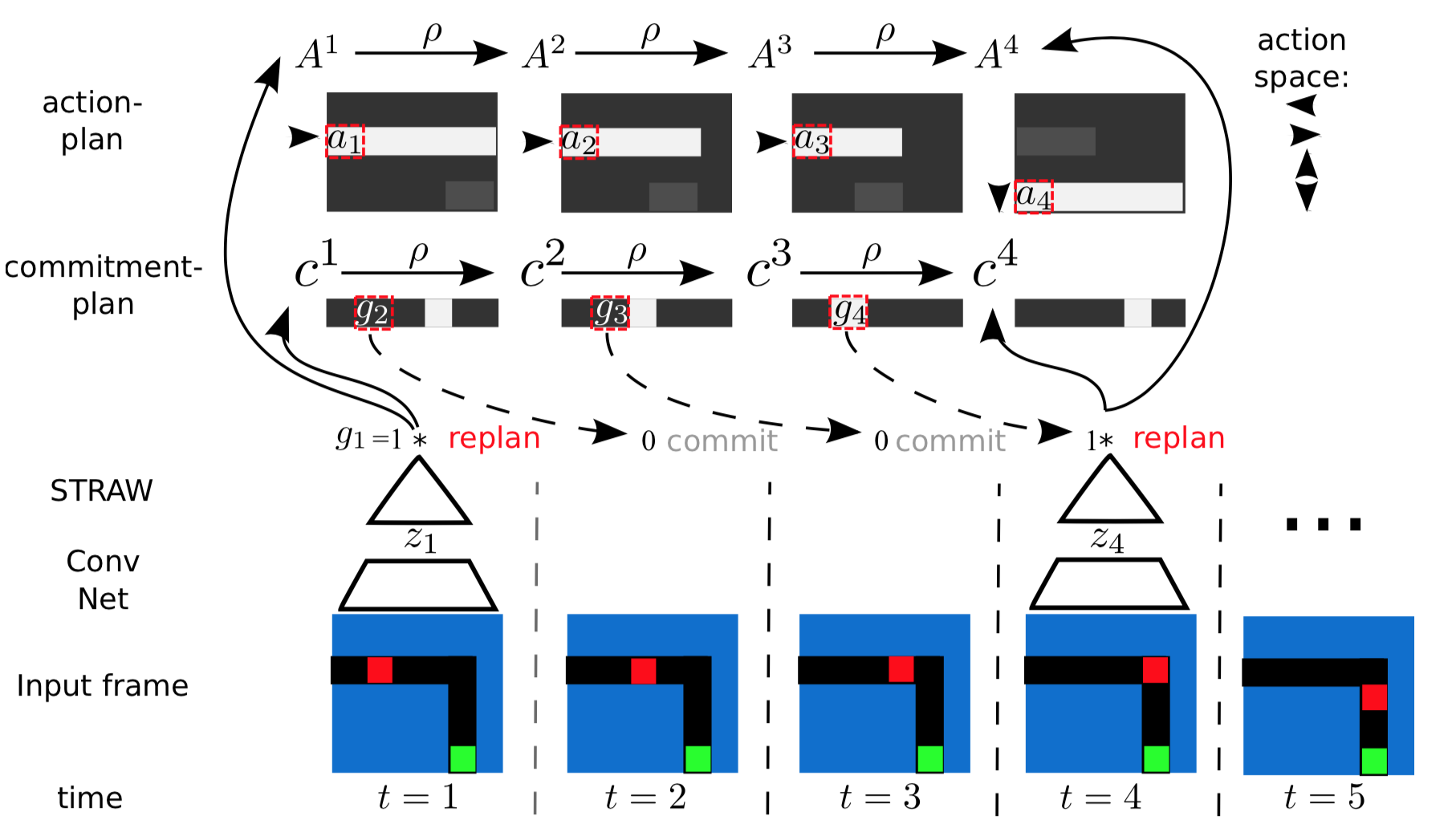
Stragetic Attentive Writer (STRAW) for Learning Macrow Actions

?We present a novel deep recurrent neural network architecture that learns to build implicit plans in an end-to-end manner by purely interacting with an environment in reinforcement learning setting. The network builds an internal plan, which is continuously updated upon observation of the next input from the environment. It can also partition this internal representation into contiguous sub-sequences by learning for how long the plan can be committed to - i.e. followed without re-planning. Combining these properties, the proposed model, dubbed STRategic Attentive Writer (STRAW) can learn high-level, temporally abstracted macro- actions of varying lengths that are solely learnt from data without any prior information. These macro-actions enable both structured exploration and economic computation. We experimentally demonstrate that STRAW delivers strong improvements on several ATARI games by employing temporally extended planning strategies (e.g. Ms. Pacman and Frostbite). It is at the same time a general algorithm that can be applied on any sequence data.?

H-DRLN

?We propose a lifelong learning system that has the ability to reuse and transfer knowledge from one task to another while efficiently retaining the previously learned knowledge-base. Knowledge is transferred by learning reusable skills to solve tasks in Minecraft. [...] These reusable skills, which we refer to as Deep Skill Networks, are then incorporated into our novel Hierarchical Deep Reinforcement Learning Network (H-DRLN) architecture using two techniques: (1) a deep skill array and (2) skill distillation, our novel variation of policy distillation (Rusu et. al. 2015) for learning skills.?

Abstract Markov Decision Processes (AMDP)

?We propose Abstract Markov Decision Process (AMDP) hierarchies as a method for reasoning about a network of subgoals. [...] An AMDP is an MDP whose states are abstract representations of the states of an underlying environment (the ground MDP). The actions of the AMDP are either primitive actions from the environment MDP or subgoals to be solved. [...] A major limitation of MAXQ is that value functions over the hierarchy are found by processing the state?action space at the lowest level and backing up values to the abstract subtask nodes (bottom-up process). [...] AMDPs model each subtask?s transition and reward functions locally, resulting in faster planning, since backup across multiple levels of the hierarchy is unnecessary. This top-down planning approach decides what a good subgoal is before planning to achieve it.?

Iterative Hierarchical Optimization for Misspecified Problems (IMHOP)

?For complex, high-dimensional Markov Decision Processes (MDPs), it may be necessary to represent the policy with function approximation. A problem is mis- specified whenever, the representation cannot express any policy with acceptable performance. [...] We introduce a meta-algorithm, Iterative Hierarchical Optimization for Misspecified Problems (IHOMP), that uses an RL algorithm as a ?black box? to iteratively learn options that repair MPs. To force the options to specialize, IHOMP uses a partition of the state-space and trains one option for each class in the partition.?

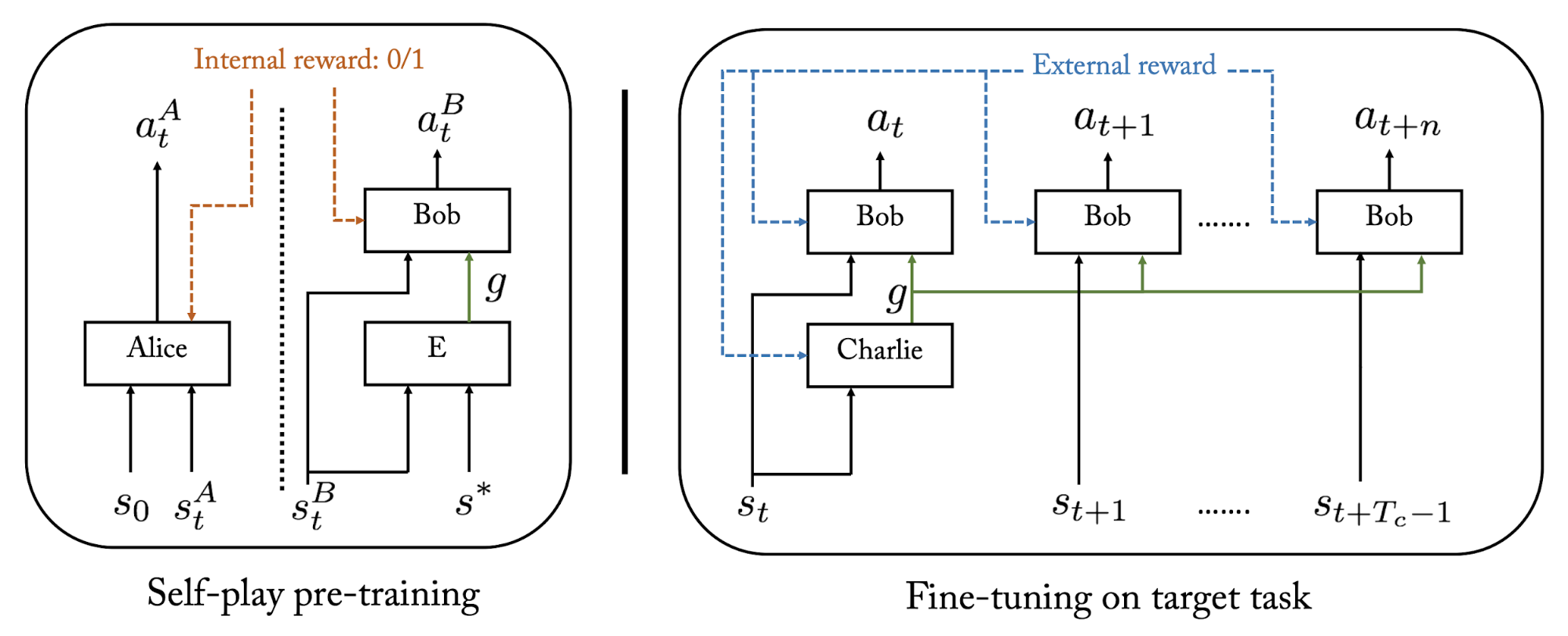
HSP

?Our approach uses unsupervised asymmetric self-play [15] as a pre-training phase for the low-level policy, prior to training the hierarchical model. In self-play, the agent devises tasks for itself via the goal embedding and then attempts to solve them. [...] A high-level policy can then direct the lower one by generating a sequence of continuous sub-goal vectors. [...] These can then be utilized in a hierarchical RL framework to speed exploration on complex tasks with sparse reward. Experiments on AntGather demonstrate the ability of the resulting hierarchical controller to move the Ant long distances to obtain reward, unlike non-hierarchical policy gradient methods. One limitation of our self-play approach is that the choice of D (the distance function used to decide if the self-play task has been completed successfully or not) requires some domain knowledge.?

Learning Representations in Model-Free HRL

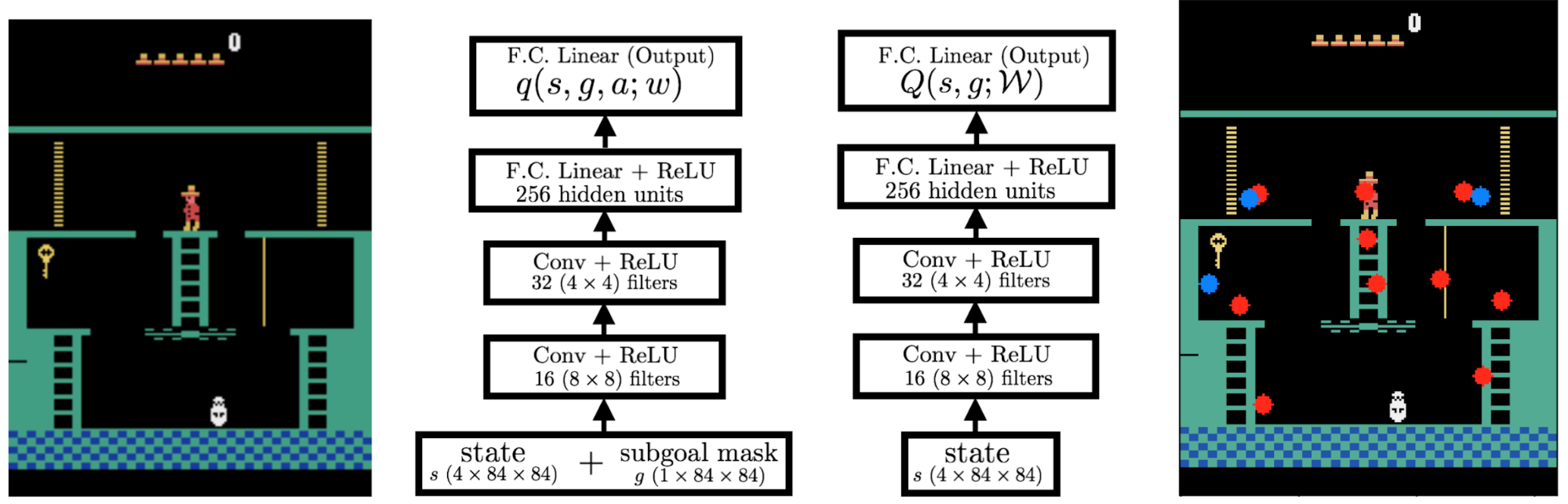
?We propose and implement a novel model-free method for subgoal discovery using incremental unsupervised learning over a small memory of the most recent experiences of the agent. When combined with an intrinsic motivation learning mechanism, this method learns subgoals and skills together, based on experiences in the environment. Thus, we offer an original approach to HRL that does not require the acquisition of a model of the environment, suitable for large-scale applications. We conducted experiments using our method on large-scale RL problems, such as portions of the difficult Atari 2600 game Montezuma's Revenge.

---

The Future of HRL

In the field of cognitive science, research ^[35][36] has long suggested that human and animal behaviour is based on a hierarchical structure. There certainly is a shift that real-world and complex environments will require us to adopt. This could be found in one of the main appealing aspects of HRL: the use of skills to reduce the search complexity of the problem.

"Stop learning tasks, start learning skills." -Satinder Singh, NeurIPS 2018

However, depending on the framework used, specifying a good hierarchy by hand requires domain-specific knowledge and careful engineering, motivating the need for learning skills automatically. Essentially, to choose an appropriate hierarchy framework one needs to look how available the domain knowledge is (a friendly combination of the three is also conceivable ^[37]):

• If the behaviours are completely specified ? Options
• If the behaviours are partially specified ? HAM
• If less domain knowledge is available ? MAXQ, Learned Options ^[24:1][32:1]

In the table below, the columns imply:

• Temporal abstraction allows representing knowledge about courses of action that take place at different time scales. We talk about temporally extended actions
• State abstraction occurs when a sub-task ignores some aspects of the state of the environment, it requires that sub-tasks be specified in terms of termination predicates as opposed to using the option or partial policy methods
• "Sub-tasks: fixed policy provided by the programmer" means given a set of options, the system learns a policy over those options
• "Sub-tasks: non-deterministic finite-state controller" means given a hierarchy of partial policies the system learns a policy for the entire problem
• Sub-tasks: termination predicate and a local reward function" means given a set of sub-tasks the system learns policies for entire problem
• A hierarchical optimal policy is a policy that is optimal among all the policies that can be expressed given the hierarchical structure
• A recursively optimal policy is a policy optimal for each SMDP corresponding to each of the sub-tasks in the decomposition

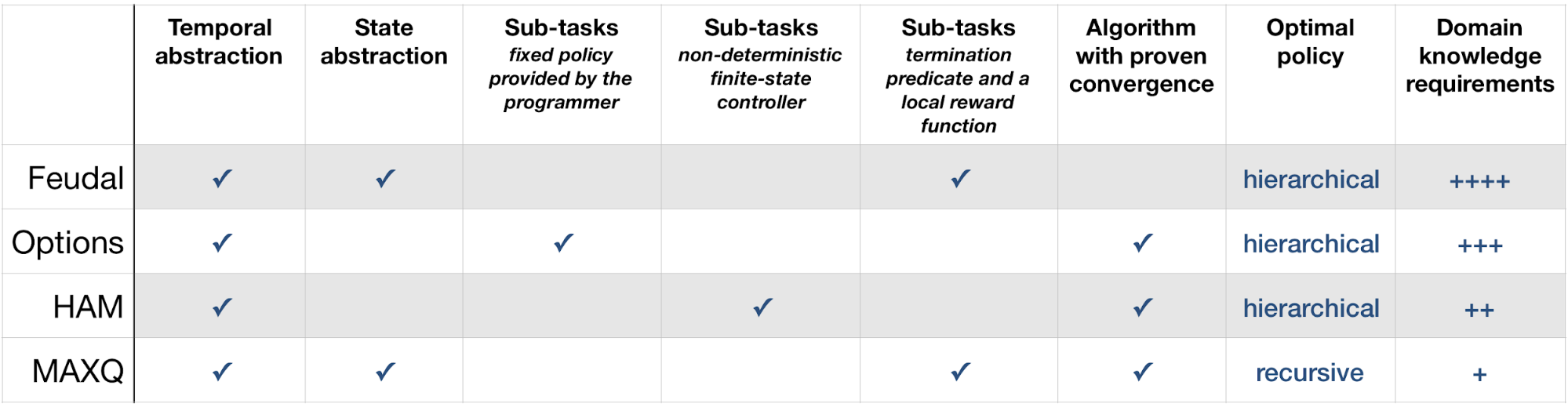
Comparison of the foundational HRL frameworks characteristics

Fundamentally, the promising benefits of HRL — faster learning by mitigating scaling problem, a powerful ability to tackle problems with large state/action by reducing the curse of dimensionality, using sub-goals and abstract actions on different tasks with state abstraction, using multiple levels of temporal abstraction, truer and better generalisation with transfer of knowledge from previous tasks — seem at reach, but not quite there yet.

There are a lot of great ideas and algorithms, but not quite a big impact or major adoption to date, and, to be honest, there is still a legitimate scepticism on the part of the RL community. On the one hand, challenges such as the non-stationarity generated by updating the levels of a hierarchical agent require more effort in implementation and introduce additional hyperparameters. On the other hand, we are still far from achieving reasonable sample efficiency, as ^[38] pointed out: in the Options framework options are atomic macro-actions independent from each other. Thus we lose the potential benefit of considering interactions between options, which could be used to significantly improve the sample efficiency. Furthermore, HRL might actually not be a necessary fix to the limitations of flat RL, as stated in the OpenAI blog-post: RL researchers (including ourselves) have generally believed that long time horizons would require fundamentally new advances, such as hierarchical reinforcement learning. Our results suggest that we haven't been giving today's algorithms enough credit - at least when they're run at sufficient scale and with a reasonable way of exploring.

Until HRL frameworks benefit from greater user-friendliness and better technical specifications, HRL will not become standard for RL problems.

That said, these defects are known issues that are precisely in line with the main active research directions in HRL, including but not bounded to:

• Better management of the non-stationarity of the higher-level state transition functions
• Learn hierarchies automatically
• More efficient exploration
• Enrich signal with efficient decomposition in environments with sparse rewards
• Improve stability

We already have observed hierarchical structures emerging in deep networks applied to perception tasks, such as computer vision with ConvNets, but these are hierarchical in the sense of perception. If we could build hierarchical temporal and behavioural systems in RL in the same way, that would have a significant impact like ConvNets had. There is still a lot of work ahead and a strong base for optimism.

What can you do from here?

If you've come this far, that means HRL is of decent interest for you. The goal of this write-up was to outline the main framework streams that served as inspiration for the subsequent contributions in HRL, to (hopefully) forge your interest for the domain if you were not familiar with it, and to encourage further discussion on the subject.

As we saw, both the Options framework and MAXQ decomposition provide algorithm designers with powerful tools to break down a problem hierarchically. Should you be interested in this line of research, you can choose the method that you think is the most promising to you, or the one that you think would benefit most from improvements. You can then develop new hypotheses to benchmark test, using open-source code (e.g. HIRO, HAC, MLSH, HSP) to build on it with new ideas, or implementing a system by yourself by drawing inspiration from the many contributions mentioned above.

To conclude on a more general point, these developments cannot be quantified if they cannot be measured properly, and I have the feeling that there is still a lack of tools to efficiently measure progress made in HRL, and more broadly in RL at all. Fortunately, the community is actively working on these issues as well. Of course, it is our responsibility to be aware of the problems inherent in our field that do not exhibit short-term difficulties but slow down progress in the long term. It is our duty to participate in their resolution and to contribute to progress in a reproducible way.

---

Special thanks to Andrey Kurenkov, Hugh Zhang, Eric Wang, Steven Ban and Florian Strub for their feedback, suggestions, and insights.
Cover image source.

---

Yannis Flet-Berliac is a PhD student at the University of Lille in the Inria SequeL team. His research project mainly involves deep reinforcement learning with a focus on stochastic and non stationary environments. Prior to starting his PhD, he worked in France and Denmark mostly on conversational models, machine translation and photographer style recognition. Find him on Twitter!

---

---

Citation
For attribution in academic contexts or books, please cite this work as

Yannis Flet-Berliac, "The Promise of Hierarchical Reinforcement Learning", The Gradient, 2019.

BibTeX citation:

@article{BerliacHierachialRL2019,
author = {Flet-Berliac, Yannis}
title = {The Promise of Hierarchical Reinforcement Learning},
journal = {The Gradient},
year = {2019},
howpublished = {\url{https://thegradient.pub/the-promise-of-hierarchical-reinforcement-learning/ } },
}

---

If you enjoyed this piece and want to hear more, subscribe to the Gradient and follow us on Twitter.

---

1. Spelke and Kinzler. Core knowledge. Developmental science, 2007. ↩︎

2. Szepesv?ri. Algorithms for Reinforcement Learning. Synthesis Lectures on Artificial Intelligence and Machine Learning, 2009. ↩︎

3. Bellemare, Dabney, and Munos. A distributional perspective on reinforcement learning. ICML, 2017. ↩︎

4. Jackson. On the comparative study of disease of the nervous system. British Medical Journal, 1889. ↩︎

5. Mussa-Ivaldi and Bizzi. Motor learning through the combination of primitives. Philosophical Transactions of the Royal Society of London B: Biological Sciences, 2000. ↩︎

6. Todorov et al. From task parameters to motor synergies: A hierarchical framework for approximately optimal control of redundant manipulators. Journal of robotic systems, 2005. ↩︎

7. Arulkumaran et al. Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine, 2017. ↩︎

8. Mnih et al. Human-level control through deep reinforcement learning. Nature, 2015. ↩︎

9. Schmidhuber. Formal theory of creativity, fun, and intrinsic motivation (1990?2010). IEEE Transactions on Autonomous Mental Development, 2(3):230?247, 2010. ↩︎

10. Pathak, et al. Curiosity-driven exploration by self-supervised prediction. ICML, 2017. ↩︎

11. Sutton and Barto. Reinforcement learning: An introduction, volume 1. MIT press Cambridge, 1998. ↩︎

12. Watkins. Learning from delayed rewards. PhD thesis. University of Cambridge England, 1989. ↩︎ ↩︎

13. Mnih et al. Human-level control through deep reinforcement learning. Nature, 2015. ↩︎

14. Currie and Tate. O-plan: the open planning architecture. Arti?cial Intelligence, 1991. ↩︎

15. Fikes, Hart and Nilsson. Learning and Executing Generalized Robot Plans. Artificial Intelligence, 1972. ↩︎

16. Knoblock. Learning Abstraction Hierarchies for Problem Solving. AAAI, 1990. ↩︎

17. Schmidhuber. Learning to generate sub-goals for action sequences. Proc. ICANN'91, pages 967-972, 1991. Based on TR FKI-129-90, 1990. ↩︎

18. Oudeyer and Kaplan. What is intrinsic motivation? A typology of computational approaches. Front. Neurorobotics, 2009. ↩︎

19. Schmidhuber. Curious model-building control systems. In Proc. International Joint Conference on Neural Networks, Singapore, volume 2, pages 1458-1463. IEEE, 1991. ↩︎

20. Sutton, Precup and Singh. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 1999. ↩︎ ↩︎

21. Dayan and Hinton. Feudal Reinforcement Learning. NIPS, 1993. ↩︎ ↩︎

22. Bacon, Harb and Precup. The Option-Critic Architecture. AAAI, 2017. ↩︎

23. Fruit and Lazaric. Exploration-Exploitation in MDPs with Options. AISTATS, 2017. ↩︎

24. Stolle and Precup. Learning Options in Reinforcement Learning. Lecture Notes in Computer Science, 2002. ↩︎ ↩︎

25. Schaul et al. Universal value function approximators. ICML, 2015. ↩︎

26. Wiering and Schmidhuber. HQ-Learning. Adaptive Behavior 6(2):219-246, 1997. ↩︎

27. Puterman. Markov Decision Processes: Discrete Stochastic Dynamic Programming, Chapter 11. John Wiley & Sons, Inc, 1994. ↩︎

28. (ie. the learnt policy will be the best policy consistent with the given hierarchy: task?s policy depends not only on its children?s policies, but also on its context) ↩︎

29. Parr and Russell. Reinforcement Learning with Hierarchies of Machines. MIT Press, 1998. ↩︎

30. Dietterich. Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition. Artificial Intelligence, 2000. ↩︎

31. Vezhnevets et al. FeUdal Networks for Hierarchical Reinforcement Learning. ICML, 2017. ↩︎

32. Bacon, Harb, and Precup. The option-critic architecture. AAAI, 2017. ↩︎ ↩︎

33. Nachum et al. Data-Efficient Hierarchical Reinforcement Learning. CoRR, 2018. ↩︎

34. (an off-policy setting is helping for sample efficiency but challenging to handle because off-policy RL creates a non-stationary problem for the higher-level policy since the lower-level is constantly changing) ↩︎

35. Botvinick, Niv and Barto. Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. Cognition, 2008. ↩︎

36. Badre, Kayser, and D?Esposito. Frontal cortex and the discovery of abstract action rules, 2010. ↩︎

37. Cai et al. A combined hierarchical reinforcement learning based approach for multi-robot cooperative target searching in complex unknown environments. IEEE, 2013. ↩︎

38. Fruit, Pirotta, Lazaric, Brunskill. Regret Minimization in MDPs with Options without Prior Knowledge. NIPS, 2017. ↩︎