Two dangerous visions

According to Engadget, 2017 was the year society started taking algorithmic bias seriously.

If it’s really true—well, better late than never. Researchers have been trying to warn us for years about the dangers of handing power to algorithms. But many people aware of the problem still don’t it seriously. These people tend to fall in one of two camps:

• The optimists, who think algorithmic reasoning is rational and objective, regardless of the situation. They might also believe that uncomfortable or undesirable results of the data simply reflect “politically incorrect” truths in the data.

• The pessimists, who think algorithmic reasoning is fundamentally flawed, and that all “truly important” decisions should be left to humans. The EU’s General Data Protection Regulation (GDPR), for instance, includes a blanket ban on fully automated decision-making in situations that “significantly affect” users.

Neither position is workable in the long run.

Optimism ignores the very real problems with algorithmic decision-making: predictive policing systems caught in runaway feedback loops of discrimination, hiring tests that exclude applicants from low-income neighborhoods, and smartphone apps that result in potholes being ignored in poorer communities are all problems that can arise from the mismanagement of algorithmic bias. Accepting outcomes like these as the best of all possible worlds seems recklessly blithe, to say the least.

On the other hand, the pessimistic vision—a wholesale ban of "important" algorithms—is simply not going to happen. Causality is a complicated thing; properly construed, a society without socially impactful algorithms is a society without “automated” services like LinkedIn (which affects where we get interviewed and hired), Facebook (whose influence on our political socialization is enormous), or Uber (which is ultimately responsible for the livelihood of many of its drivers). A world suddenly deprived of all such services is not obviously better than the one we live in now; the weaknesses of human judgment and the massive, fast-accumulating amounts of data in the world mean that algorithms are here to stay.

The importance of conceptual work

Given that algorithms are here to stay, but also the dangers of biased algorithms, it’s necessary to think deeply and critically about how we can make algorithms work in unbiased ways.
While corporations and governments may be willing to work to remove bias from their algorithms, their actions should be grounded in a consistent understanding of what bias is and how it happens. Without a formal theory of bias, the field is open—to optimists who claim that the algorithm “really isn’t biased” for some contrived reason, and to pessimists who insist on satisfying mutually contradictory measures of fairness.

The burgeoning literature on fair machine learning is full of individual corrections, adjustments, and constraints that could potentially “debias” algorithms. But many of these corrections fail to justify themselves through an explicit theory of what bias is and how it can enter an algorithm.

This absence of a larger framework makes sense—the fundamental questions of truth, justice, and fairness that any such framework must address have historically lay within philosophy, not statistics or computer science. Still, as long as domain knowledge remains concentrated in the technological community, the burden of conceptualizing bias falls at least partly on the technologists.

This is no easy feat. It involves making the implicit assumptions of technical papers explicit, distilling these assumptions into their core principles, and reflecting on the soundness of these principles.

Still, a few attempts have been made in the last few years toward this conceptual feat. This article examines two of these formal models of bias that have appeared relatively recently. One I'd call epistemic, and the other I'd call utilitarian. But before we get into them, we need a concrete example to show why they’re necessary.

The curious case of word embeddings

In an article published last year in Science, Caliskan, Bryson, and Naranayan pointed out one of the most famous and striking examples of algorithmic bias: biased word embeddings.

A word embedding is a model that maps English words to high-dimensional vectors of numbers. The model is trained on large bodies of text to correlate semantic similarity with spatial proximity. That is, words with similar meanings should have embeddings close to each other. This property makes them useful in natural language processing.

To prove that there was social bias lurking in these embeddings, the authors propose something called the Word Embedding Association Test (WEAT), an analogue of the famous Implicit Association Test for subconscious social biases.

The details of the WEAT are as follows. Borrowing terminology from the IAT literature, consider two sets of target words (e.g., programmer, engineer, scientist; and nurse, teacher, librarian) and two sets of attribute words (e.g., man, male; and woman, female). The null hypothesis is that there is no difference between the two sets of target words in terms of their relative similarity to the two sets of attribute words. The permutation test measures the (un)likelihood of the null hypothesis by computing the probability that a random permutation of the attribute words would produce the observed (or greater) difference in sample means.

Like the IAT, the WEAT found an abundance of statistically significant social biases in its subjects. A sample:

• Male names and pronouns were closer to words about career, while female ones were closer to concepts like homemaking and family.
• Young people’s names were closer to pleasant words, while old people’s names were closer to unpleasant words.
• Male names were closer to words about math and science, while female names were closer to the arts.

These results point to historical inequality. Embeddings measure the similarity between two words by how often they occur near one another; if most doctors historically have been male, for instance, then words like doctor would appear near male names more often, and would be associated with those names.

The standard concern is that the machine might reproduce this inequality. For instance, a résumé-screening algorithm that carelessly used word embeddings to measure how “professional” or “career-oriented” a candidate was might unfairly discriminate against female candidates, simply on the basis of their names.

A projection of word embeddings. The x-axis is parallel to $v_{he} - v_{she}$; the y-axis measures the strength of the gender association. Photo from Man is to Computer Programmer as Woman is to Homemaker?.

In 2016, in response to this apparent inequality, Bolukbasi et al. invented a simple and effective technique to “debias” word embeddings.

Consider the difference between the vectors for he and she. This difference is a vector that can represent some notion of “gender.” If you did this for male/female, father/mother, and actor/actress, you would get similar “gender” vectors, something like the he-she axis in the graph above. In practice, these vectors are rarely parallel, but they’re close; we can imagine them lying in a certain “gender subspace” that captures the differences between the gendered variations of a word.

From a technical standpoint, the algorithm in the paper identifies this subspace by running a principal component analysis on the gender vectors. Then it uses vector projections to remove the variation within this gender subspace for gender-nonspecific words, stripping away their gender associations.

This approach can be generalized to any social bias: simply take groups of words that should have equivalent meanings aside from some social factor like religion, or nationality, and use their difference to approximate the corresponding subspace. (What kind of meaning might lie in the vector between Joe and José?)

To debias or not to debias?

But the technique leaves open the most important questions. What is the nature of the bias that this algorithm removes, and why is this the correct way to remove it? When should we debias, and why should it be done in this way, and not others?

We need to think more deeply before we can decide whether “debiasing” is even a coherent concept. It certainly appears to address one of the symptoms of bias, but it does this by smudging away certain dimensions of the data in potentially unhelpful ways. Arvind Naranayan, one of the authors of the paper on biased embeddings, notes that the issue of debiasing isn’t as straightforward as it seems: “What constitutes a terrible bias or prejudice in one application might actually end up being exactly the meaning you want to get out of the data in another application.”

This statement is a natural consequence of the fact that there is no such thing as an inherently biased measurement.

“Biased” data and biased estimators

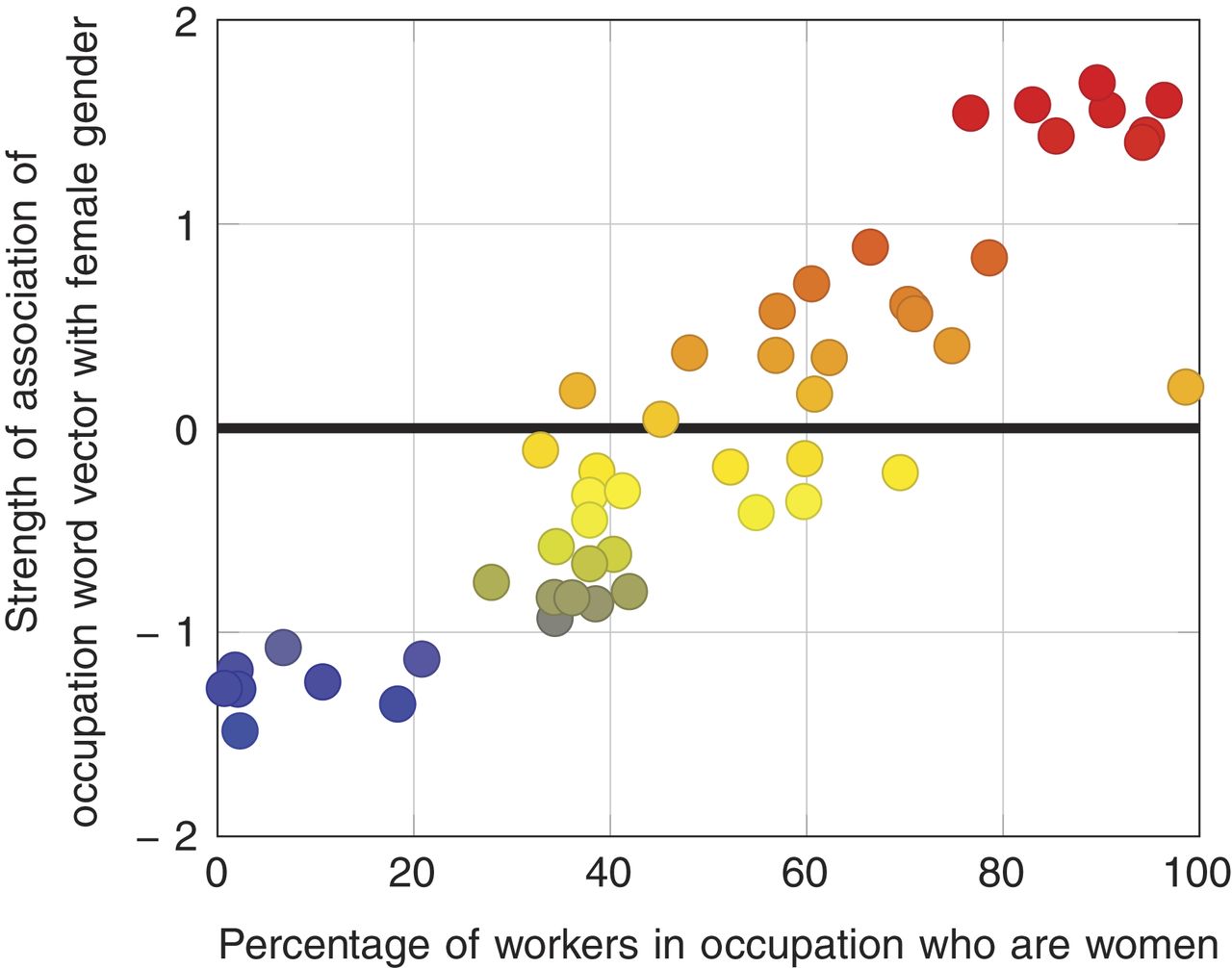
Photo from Caliskan et al.

An SAT score is an unbiased measurement of how skilled someone is at taking the SAT. An IQ test is an unbiased measurement of how well someone does on an IQ test. Even the notorious literacy tests used by state governments in the South were a pretty decent measurement of, well, how much people wanted you to vote.

But the standard criticism of SAT, IQ, and literacy tests is that they are often interpreted as proxies for other important yet intangible factors—of future performance in college, of human potential, of the validity of someone’s political opinions. A measurement can only be “biased” insofar as it purports to measure something else.

Word embeddings are unbiased estimators of certain arbitrary mathematical properties of the English language as it was used over the past century or two. They are not unbiased estimators of the words’ dictionary definitions, let alone their "meaning."

Consequently, there are valid and invalid interpretations of what they mean.

If you were a scholar in the digital humanities looking to track the relative proportions of male and female characters in English-language novels over the past three hundred years, it would make little sense to remove the algorithm’s understanding of the gender imbalances in certain occupations. If you were a data scientist trying to determine the sentiment of online comments, you might want to be able to pick up on the negativity in a 14-year-old’s snide comment that “this video is gay.” If you were trying to parse some Romantic poetry, you probably don’t want your algorithm to trip up when Wordsworth refers to nature as a “she.”

But you would run into serious problems in other situations. In the context of the résumé-screening task, a system that estimates the “professionalism” of a candidate through the proximity of the words in their résumé to career words would fail disastrously in providing an unbiased estimate.

This insight—that what an estimator claims to estimate is just as important as the estimator itself—can be developed into our first formal theory of algorithmic bias.

Theory 1: constructs, axioms, and algorithmic bias as biased belief

One conception of algorithmic bias is based on a statistical interpretation of “bias.” This is the idea that people typically have in mind when discussing algorithmic bias in predictive policing: if crimes committed by one group are more likely to be reported than those committed by another, we can say that reported crime is a biased estimator of true crime rates. And if we accept that the estimator is biased, an algorithm that used it without correcting for this bias would probably be biased against certain communities.

Now, there’s a lot that can be done to remove bias from estimators. Social scientists, for instance, are notoriously circumspect about this. But in many cases, there’s no way to reach an estimate without the possibility of bias. Maybe, like the crime-rates example, there’s simply no way to observe the information you need. Maybe a large swath of your population wants to avoid interactions with formal institutions. Or maybe you’re trying to estimate something intangible, like friendliness or professionalism, where the ground truth is inherently impossible to measure.

This is enormously frustrating for a machine learning practitioner. How do we know anything if we don't trust our data?

Maps and Spaces

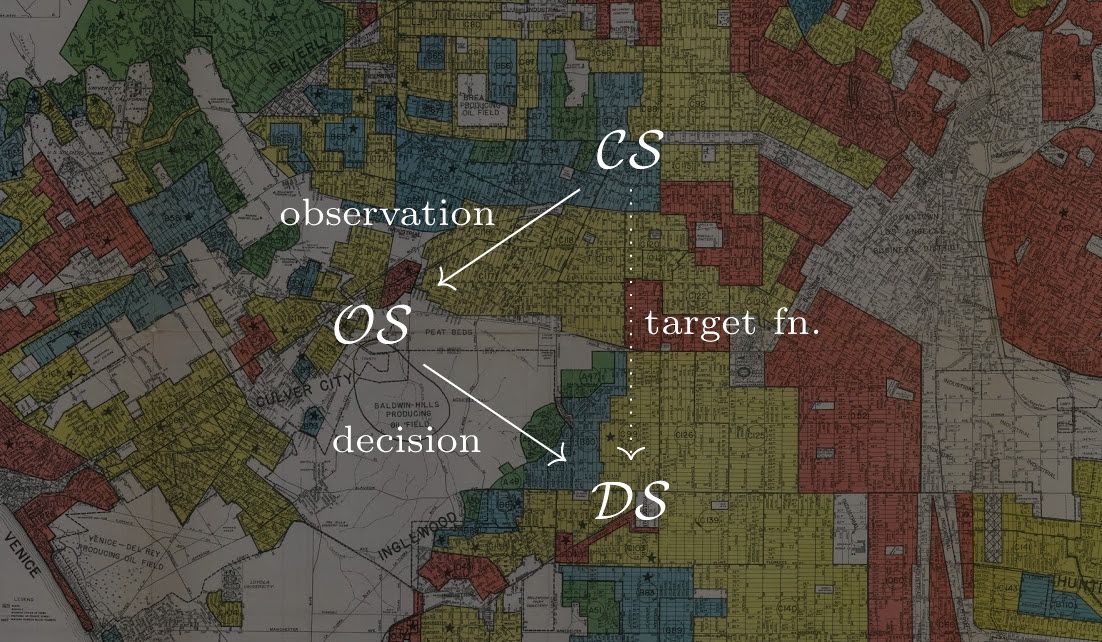
This question motivates Friedler, Scheidegger, and Venkatasubramanian (2016) in their attempt to answer the question of what bias is. The paper aims to build a theoretical framework for fairness-aware algorithms by modeling algorithms as maps:

Our primary insight can be summarized as: to study algorithmic fairness is to study the interactions between different spaces that make up the decision pipeline for a task.

In their model, an algorithmic decision-making pipeline is a mapping between three metric spaces:

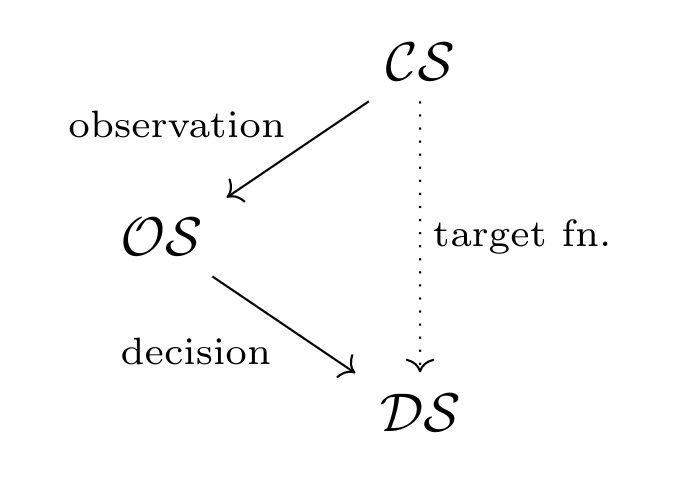
• $\mathcal{CS} = (P, d_P)$, or the construct space. This space holds the inaccessible, ideal features that are relevant to the task.
• $\mathcal{OS} = (\hat P, \hat d)$, or the observed space. This is the space that the algorithm has access to. The observations are generated from the construct space by a possibly noisy process, and they may or may not reflect the construct space well.
• $\mathcal{DS} = (O, d_O)$, or the decision space. These are the concrete outcomes that the algorithm assigns.

For instance, a university may want to choose whether to accept, reject, or defer an applicant ($\mathcal{DS}$) based on how intelligent and hardworking they are ($\mathcal{CS}$). However, only have access to the applicant’s high school GPA and essays ($\mathcal{OS}$), which may or may not be a good estimator of the applicant’s intelligence or industriousness.

More generally, the goal of the algorithm designer is to learn a specific function from $\mathcal{CS}$ to $\mathcal{DS}$. However, all we have available to us are features from the observation space, $\mathcal{OS}$, whose connection to the construct space $\mathcal{CS}$ is unproven. Thus, our learning algorithm can only try to determine a suitable mapping from $\mathcal{OS}$ to $\mathcal{DS}$.

With this in mind, the authors lay out their definition of fairness:

A mapping $f : \mathcal{CS} \rightarrow \mathcal{DS}$ is said to be fair if all objects that are close in the metric space $\mathcal{CS}$ are also close in the decision space $\mathcal{DS}$. [The authors proceed to restate this more rigorously.]

A fair algorithm should map two individuals who are similar in the construct space to similar outcomes in the decision space. If two applicants are equally hardworking and intelligent, they’ll be equally likely to be accepted to a university under a fair model. Because the original goal was to learn a well-defined function from $\mathcal{CS}$ to $\mathcal{DS}$ anyway, we should always strive to be fair.

But fairness is only possible if the observation space actually reflects the construct space accurately. If your observation space reflects something else entirely (for instance, the wealth of a college applicant’s family), then “fairness” is simply impossible.

So let’s return to our original question: how is it possible to learn from unreliable data? Before it can make any justifiable decisions, a statistical model needs to assume something to be true about the construct space—a trusted dataset, a modeling assumption, or even a prior. The authors identify two such assumptions, called "worldviews," used implicitly or explicitly in the fairness literature:

The WYSIWYG (What You See Is What You Get) axiom

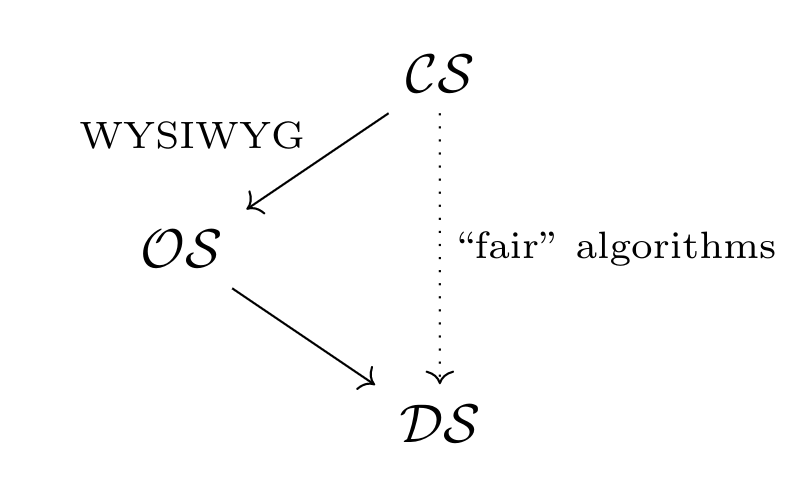
This worldview holds that the observed space is a reasonable reflection of the construct space. More concretely, it holds that there exists a mapping $f: \mathcal{CS} \rightarrow \mathcal{OS}$ such that the distance between two points changes by at most some small $\epsilon$. This is known as the WYSIWYG axiom, and it’s another way of saying what most machine learning practitioners already believe: you can trust your data.

However, you can’t always trust your data. That’s why fairness-aware algorithms are more often built on what the authors call the structural bias worldview.

The WAE (We’re All Equal) axiom

As we’ve seen, many estimators can be statistically “biased.” The structural bias worldview accounts for this by taking for granted that different groups in the construct space are represented differently in the observed space.

The authors model this by considering population groups as a partition of each space. The bias is captured in the mapping between two spaces as group skew, a mathematical measure which captures how differently different groups are transformed by a mapping between spaces. The notion of group skew enables us to finally define several key concepts in the field:

• Structural bias refers to high group skew between $\mathcal{CS}$ and $\mathcal{OS}$.
• Direct discrimination refers to high group skew between $\mathcal{OS}$ and $\mathcal{DS}$.
• A non-discriminatory system exhibits low group skew between $\mathcal{CS}$ and $\mathcal{DS}$.

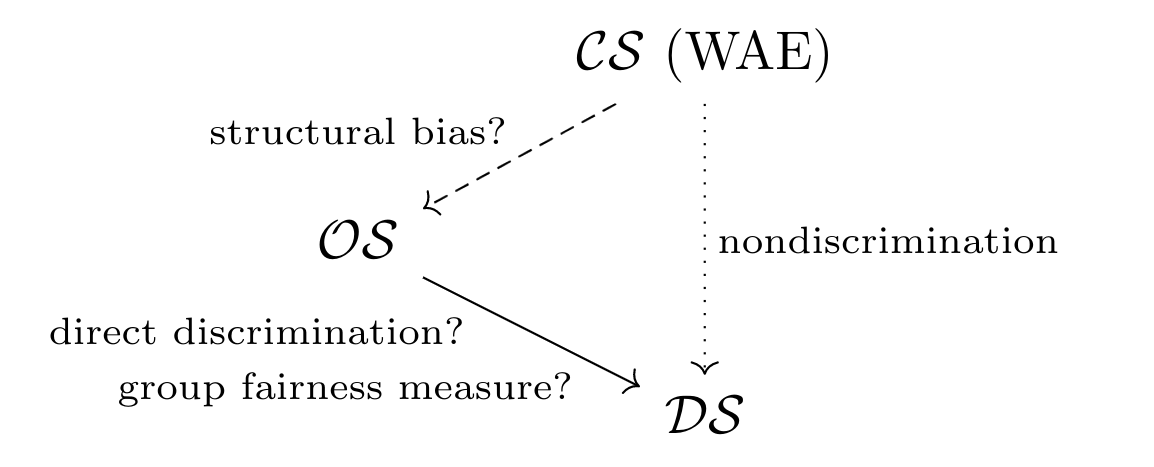
But how can we even try to approximate some function of the construct space when we have no reliable information about it? The answer is the WAE (We’re All Equal) axiom. Informally^[1], the authors explain it thus:

[A] common underlying assumption of this worldview, that we will make precise here, is that in the construct space all groups look essentially the same. In other words, it asserts that there are no innate differences between groups of individuals defined via certain potentially discriminatory characteristics. This latter axiom of fairness appears implicitly in much of the literature on statistical discrimination and disparate impact.

If we think through the implications of this axiom, it means that:

• All of the population groups are similarly distributed with respect to the constructs that your decisions are “based on” (the WAE axiom);
• The differences between these groups in the observed space is solely due to biased observations of the construct space (structural bias);
• The goal is to correct for this structural bias in such a way that group skew is minimized between the construct space and the decision space (non-discrimination).

But because the groups are distributed equally in the construct space, non-discrimination really means that we need to distribute them equally in the decision space, too. Thus, the WAE model provides a theoretical justification for fairness constraints like the 80% rule, which require job applicants from different groups to be hired at roughly equal rates. WAE holds that a workable way to ensure nondiscrimination (but not necessarily fairness) is to enforce roughly equal outcomes between groups.

Issues with the theory: biased belief can’t explain everything

But it seems odd and indirect to address social inequality by telling our algorithm that it doesn’t exist. To be fair, the authors argue that assuming the axiom doesn’t necessarily mean that the group distributions are equal:

In this [alternative] interpretation, the idea is that any difference in the groups’ performance (e.g., academic achievement) is due to factors outside their individual control (e.g., the quality of their neighborhood school) and should not be taken into account in the decision making process.

...

Since the construct space is the space of features used for ideal decision-making, in this case potential, intelligence, and diligence might be assumed to represent an idealized belief of the characteristics and abilities of an individual were their class background equalized. (Some may believe that this case is the same as representing these qualities at the time of birth.) This would be a choice to follow the WAE axiom.

This still seems slightly off. Say the admissions officer wants to admit the most academically prepared students, but also for the university to serve as a social equalizer. Because we’ve formulated structural bias as biased belief, there’s only one way to express both of these goals in the three-space framework: we must say that the admissions officer wants to admit the students that were most academically prepared at birth.

This is absolutely not how people actually think. Is a socially conscious bank manager supposed to give loans to people based on how ideally solvent they would have been if class didn’t exist? Is a scholarship committee supposed to award money to those who were most promising at the time they were born? These construct spaces might explain their behavior, but they have no relation to the actual intent behind this behavior. So how can we create a model that accounts for intent?

Theory 2: utilitarianism, optimization, and algorithmic bias as biased action

Forget the construct space: formal fairness requirements are costly

Corbett-Davies et al. (2017) highlight an important aspect of machine learning algorithms that the “three-space” model generally ignores: more often than not, algorithms are part of a larger system, with a very specific task to accomplish.

Sure, university admissions departments might be making grand philosophical decisions about which personal qualities they want to use to select students. But for every university admissions department, there are a hundred corporate data scientists who have been tasked with maximizing advertising clicks or minimizing retraining costs, regardless of what data is used to make that conclusion.

In these situations, the choice of construct space doesn’t matter nearly as much as some concrete objective that the algorithm is trying to optimize. This demands a different understanding of fairness that is unconcerned with the construct space:

Here we reformulate algorithmic fairness as constrained optimization … Policymakers wishing to satisfy a particular definition of fairness are necessarily restricted in the set of decision rules that they can apply. In general, however, multiple rules satisfy any given fairness criterion, and so one must still decide which rule to adopt from among those satisfying the constraint. In making this choice, we assume policymakers seek to maximize a specific notion of utility.

The paper examines a hypothetical algorithm that decides whether or not a criminal defendant should be detained or released while awaiting trial, based on a statistical model that estimates the likelihood of recidivism given “all of the available features for each defendant, excluding race.” (The authors also note that adding race didn’t help.)

The policymaker designing our algorithm must balance two considerations. The first is the immediate utility of the algorithm’s choices: the benefits of preventing violent crime, balanced by the social and economic costs of jailing. The second is the long-term fairness of the algorithm’s choices: if maximizing immediate utility results in jailing one group significantly more than another, then the algorithm will only exacerbate social inequalities through its effects, ultimately causing a net harm to society. From a utilitarian perspective, fairness can therefore be boiled down to preventing the social harm caused by worsening inequality.

To guarantee long-term fairness in situations involving human-level decisions, a number of concrete fairness constraints have proposed in the broader literature, such as:

• Statistical parity: the average outcome for each group is the same.
• Conditional statistical parity: controlling for a select few “legitimate” observations, the average outcome for each group is the same.
• Predictive equality: the “false positive rate” (say, the proportion of people jailed in error) for each group is the same.

Thus, in many cases, the problem can be reduced to constrained optimization: specifically, picking the “decision rule” that maps observations to actions with maximum immediate utility, under some formal fairness constraint.

When we do frame fairness as a constrained optimization problem, however, another aspect of it becomes apparent: fairness has a cost, and the cost isn’t negligible. By cross-validating on crime data collected in Broward County, Florida, the authors found that training a decision rule under the fairness constraints above can lead to increases of 4-9% in violent recidivism, compared to an unconstrained decision rule. On the other hand, "optimally" detaining 30% of defendants means detaining 40% of black defendants, and only 18% of white defendants. This is an equally repugnant conclusion that the authors call "the cost of public safety."

(Importantly, these statistics are based on data that may be biased. And unlike in our first theory, we have no way of accounting for this effect here.)

There is … an inherent tension between minimizing expected violent crime and satisfying common notions of fairness. This tension is real: by analyzing data from Broward County, we find that optimizing for public safety yields stark racial disparities; conversely, satisfying past fairness definitions means releasing more high-risk defendants, adversely affecting public safety.

For a policymaker, the respective costs of fairness and public safety represent the tensions between optimizing for short- and long-term utility: do we choose to maximize public safety right now, at the cost of an inequitable future?

There are other, less tangible costs, too. The authors prove that the optimum decision rule for an unconstrained algorithm is to set a uniform threshold of risk, and then to jail any defendant with a recidivism probability greater than that risk. Algorithms satisfying fairness constraints, on the other hand, need different thresholds for different population groups—”fairness through awareness.” It’s likely that this conception of fairness might not survive a confrontation with federal discrimination legislation, which demands equal treatment under the law.

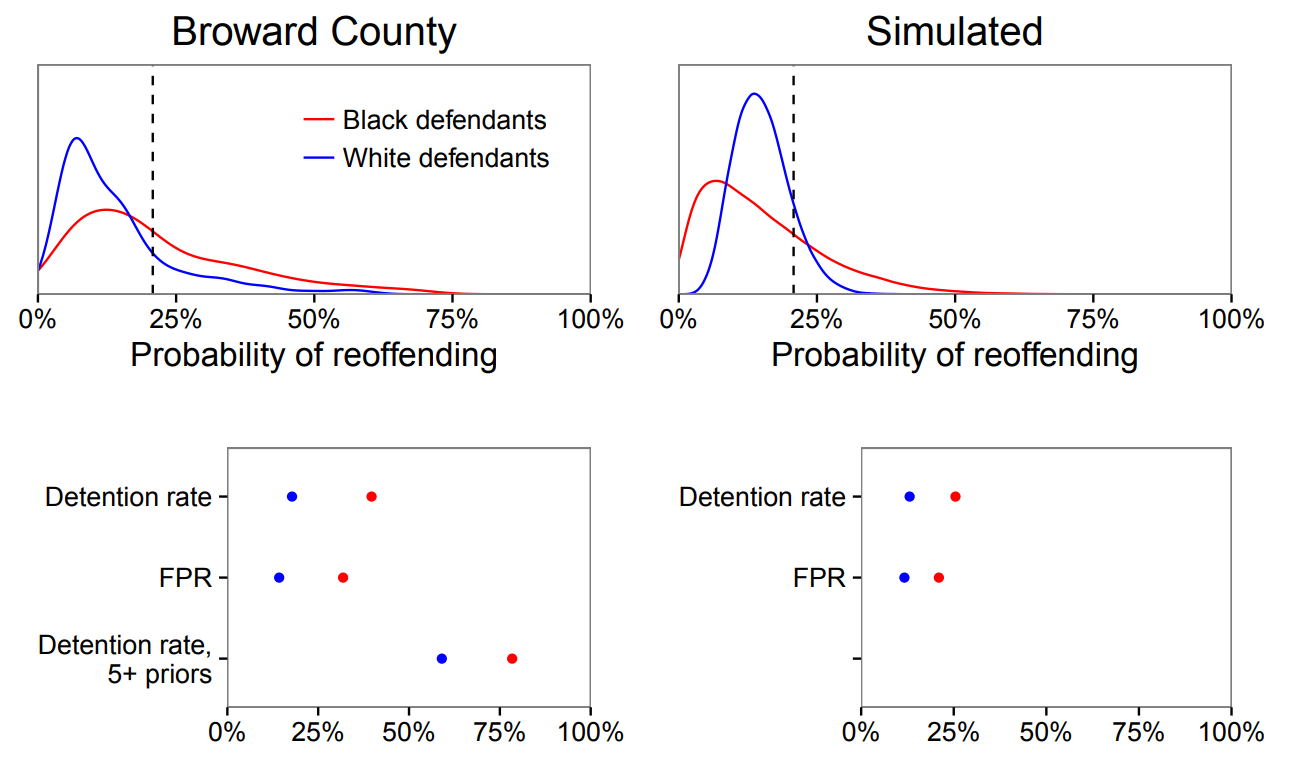
[The impact of a uniform risk score threshold on different fairness measures. We see that statistical parity (equal detention rate), predictive parity (equal false positive rate), and conditional statistical parity (equal detention rate given legitimate priors) are all unsatisfied. Diagrams from Corbett-Davies et al.]

But the most concerning thing about the authors’ cost-benefit perspective on fairness is the simple fact that the cost of fairness makes it unlikely that private corporations would have any incentive to make their algorithms fair. It’s profitable for companies to detect and use social inequalities to their advantage; if a tech conglomerate could get away with showing ads for high-paying jobs to men and showing ads for purses to women, they would. And as socially harmful as these individual actions may be in the long run, they can result naturally from the unconstrained optimization for profit.

And how do we account for biased belief?

The constrained optimization model suffers from the opposite problem from the three-spaces model: by modeling bias as biased action, it relies completely on the “WYSIWYG” assumption that its statistical estimators are valid. While the authors offer some justification of that assumption in their paper, it’s unclear whether these estimators are quite as easily verified in the general case.

Necessary, but not sufficient

Formal theories are necessary if we want to enjoy the benefits of algorithms without the drawbacks of algorithmic bias. But the conceptual frameworks that have been proposed—one a framework of bias as biased belief, and the other of bias as biased action—are almost completely opposite. Each has its benefits and drawbacks, and it isn’t clear at the moment whether a coherent synthesis of them is possible.

But regardless of which framework (if either) prevails, they are only a first step. Definitions of fairness are only useful if someone actually wants to introduce fairness to their algorithm. And if fairness is costly, then we have no reason to expect that any of the techniques we develop to address bias will actually be used.

A serious solution to algorithmic bias needs to be not only technical but also legal. Otherwise, an unchecked market with access to increasingly powerful predictive tools can gradually and imperceptibly detect and worsen social inequalities.

In the end, algorithmic bias is a lot like climate change. It’s a massive, decentralized threat, it’s trivially easy for anyone to contribute to, and certain large companies have a lot to lose if we clamped down on it. But disaster awaits if we fail to address it soon, and conceptualizing bias, like doing climate science, is necessary but not sufficient.

---

Citation
For attribution in academic contexts or books, please cite this work as

Eric Wang, "What does it really mean for an algorithm to be biased", The Gradient, 2018.

BibTeX citation:

@article{ewang2020bias,
author = {Wang, Eric},
title = {What does it really mean for an algorithm to be biased},
journal = {The Gradient},
year = {2018},
howpublished = {\url{https://thegradient.pub/ai-bias// } },
}

---

If you enjoyed this piece and want to hear more, subscribe to the Gradient and follow us on Twitter.

---

1. Formally, the WAE axiom states that the Wasserstein distance between the different population groups in the construct space is bounded above by some small constant. ↩︎