Symmetries, Scaffolds, and a New Era of Scientific Discovery

The Challenge of Drug Discovery

The development of new medicines is often laborious, time-consuming, costly, and prone to failure. The failure rate is notoriously high, with the most recent statistic being 90% [1,2]. The range of potential drug-like molecules is estimated to be between $10^{23}$ and $10^{60}$, resulting in a large and discrete search space, while it is predicted that “only” about $10^8$ molecular substances have been synthesised [3]. The chemical space of molecular candidates is vast, and within this space, interesting and powerful drugs are waiting to be found.

Impactful drugs, like the discovery of thalidomide or penicillin, have changed the course of medicine and shaped the field. However, the first drug is notorious for being part of the thalidomide tragedy, which caused birth defects and deaths among pregnant women in the 1960s [4]. The root cause was ignored handedness (or, in jargon, the chirality) between the molecular compounds, i.e. molecules that are non-superimposable on their mirror images with regards to a symmetry axis [5]. A left-handed compound might have different pharmacological properties than a right-handed compound; could it yield a toxin, or could it yield the next “wonder drug”?

The study of symmetry, along with a better understanding of the functioning of the molecules, is therefore vital to the drug development pipeline. However, existing research is predominantly focused on the study of 1-D and 2-D molecular representations, instead of leveraging the full geometrical information within these models. Developing tools to leverage the geometrical information and efficiently navigate the search space is one of the core challenges in modern chemistry. Fortunately, the field of geometric deep learning, a field that exploits the symmetries of machine learning models in non-Euclidean domains [6], is increasingly being used to speed up nearly every stage of the drug development pipeline. From the prediction of the physicochemical properties of a particular compound to clinical development, while respecting the geometry of the task at hand [7] -- they all contribute to addressing the grand challenges facing drug discovery. This article will cover how the application of geometric deep learning and the field of molecular machine learning is ushering us into a new era of scientific discovery.

A Brief History of Computer-Aided Drug Discovery

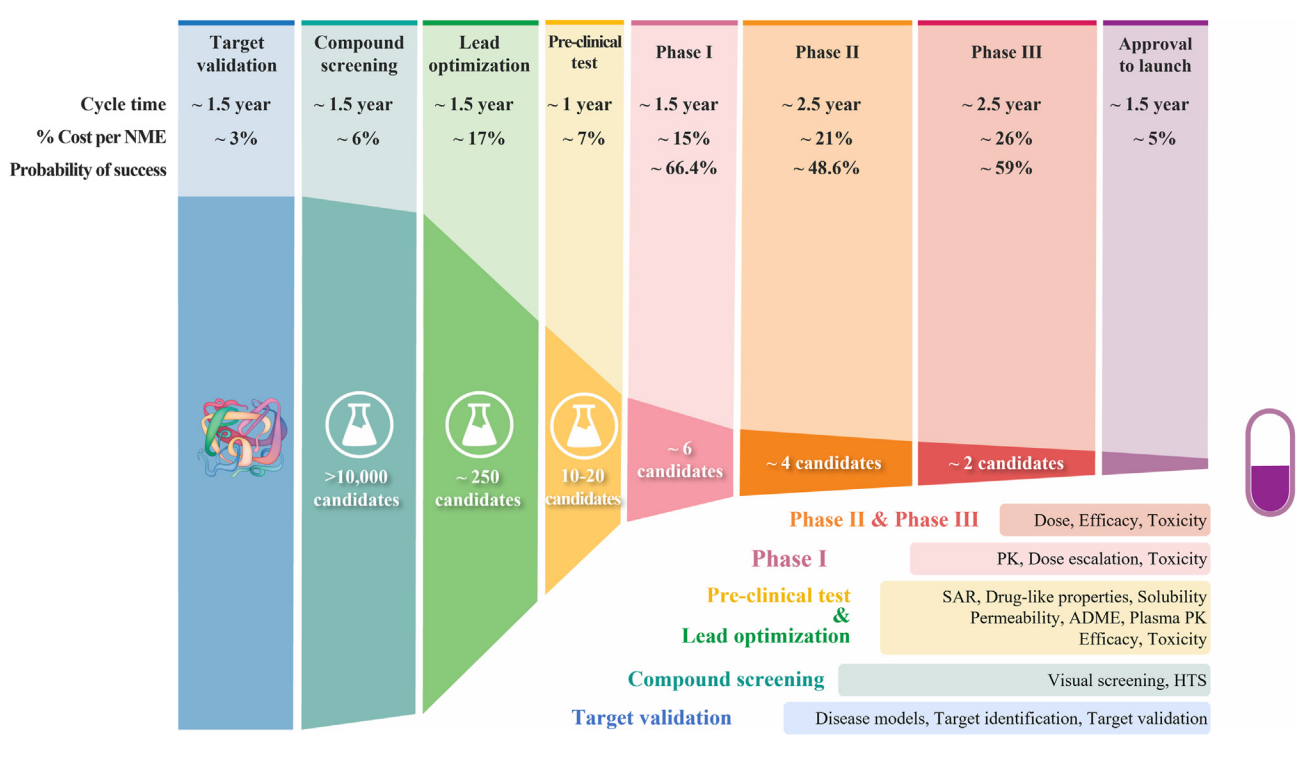
For the past three decades, computer-aided discovery and design methods have been a significant contributor to the development of relatively small, therapeutic molecules [8]. Ever since, there has been a considerable increase in the amount of public quantitative molecular bioactivity data and biomedical data on the effects of a molecule on a living system [9,10].  Due to this steep increase in the amount of data, it quickly becomes infeasible to mine knowledge by hand to generate new insights; automated tools, such as machine learning algorithms, form one solution to this problem. Simplified correlations can be inferred between the input elements that retain the necessary information required to get to the desired outcome. This gives room to accommodate more data, however, explainability and scientific accuracy (not statistical accuracy) can be compromised.

The use of deep learning has proven to be highly successful in data-rich fields such as computer vision, natural language processing, and speech recognition [11]. Building upon these successes, deep learning is increasingly being applied to problems in the natural sciences, which includes the field of chemistry. Traditional advances in chemistry have combined the implementation of novel experiments with analytic theory, which mirrors the classical scientific method by developing falsifiable hypotheses. Now, as we are steering more into the era of big data, computer-aided approaches are gradually being applied to accelerate our scientific research and understanding. Similarly, these methods allow for data-driven research that generates falsifiable hypotheses which are then tested [12].

Data-driven applications have increasingly been shown to accelerate solving diverse problems in the drug discovery pipeline [13] -- from the use of predictive analytical methods in high-throughput screening to the use of generative models for discovering and designing novel compounds. While the exploration of the chemical space is beneficial, it unfortunately lacks the ability to discover novel and unknown chemical compounds. The main reason for this is that the current chemical space, which is merely a fraction of the active chemical space, is limited to established, well-known compounds.

One of the most significant advances in the field of molecular machine learning is the ability to predict the physicochemical properties of specific drugs. The first approach included the use of Quantitative Structure-Activity Relationship (QSAR) models. These models use molecular descriptors to predict the physicochemical properties and biological activities of molecular compounds in regression and classification tasks [14]. Through advances in artificial intelligence, the paradigm shifted more to the use of deep learning models. Classical machine learning methods, such as regression models, still outperform deep learning methods at certain complex benchmark tasks due to the limited data availability [15].

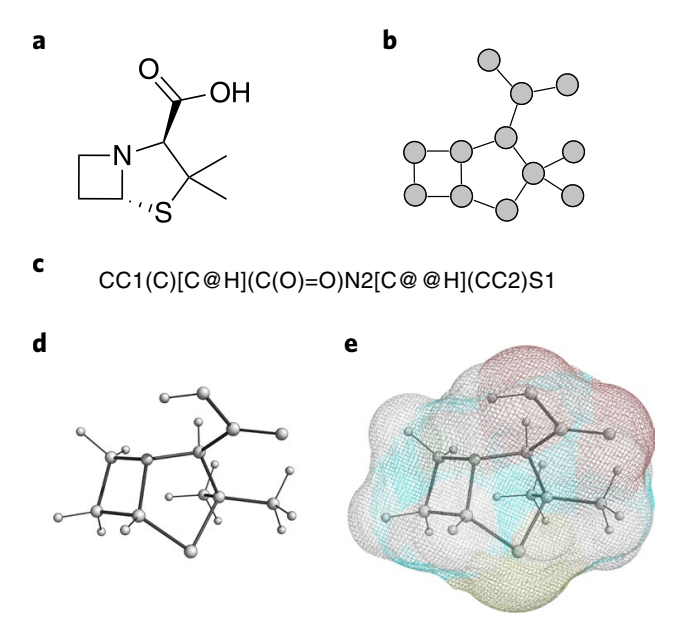
We can represent molecular structures in several distinct ways, as seen in Figure 2. Developing a one-size-fits-all and generalizable solution is a significant challenge, as these representations capture and reflect different valid configurations of the same molecular instance. To this end, existing methods from natural language processing have been adopted, such as the use of sequence-based models (e.g. recurrent neural networks [18] and Transformers [19]) to tackle 1D and 2D structures, or graph neural networks (GNNs) for handling 3D representations. There can be many simplified molecular-input line-entry specification (SMILES) strings that all represent the same graph, while a recurrent model needs to learn to map all valid permutations of the SMILES string to the same output. A GNN, which inherently respects permutation symmetries, handles this more elegantly.

The properties and interactions of a molecule are not only based on the interatomic bonds and the information provided in a molecular graph, but are also determined by the underlying physical interactions between the atoms, which depend on their 3D geometry [20]. Because of this, 3D molecular representations encode the full geometry of the molecule and thus bring in more information. This is especially useful when determining whether a molecule is the right fit for a binding receptor on a cell membrane.

Including 3D information about molecules as additional input to a machine learning model is expected to result in a more expressive and realistic method of defining their dynamics. The field of geometric deep learning (GDL) allows us to leverage the intrinsic geometrical features of a molecule and enhance the quality of our models. In recent years, GDL has repeatedly proven to be useful in generating insights on relevant molecular properties, as a result of its natural feature extraction capabilities, which will be discussed below [6].

Symmetries, Chiralities, and Geometric Deep Learning

Physical systems and their interactions are inherently equivariant [21]: orientations within the system should not change the physical laws that govern the behaviour and properties of interacting elements. In the field of GDL, symmetry is considered to be an indispensable topic, as it encompasses the properties of an arbitrary coordinate system with respect to transformations such as translations, reflections, rotations, scalings, or permutations [17].

Traditional machine learning models make no assumption of symmetry (and hence, are not symmetry-aware), and are sensitive to the choice of coordinate system. To be able to recognize an n-dimensional pattern in any orientation, such a model needs to explicitly be passed every possible configuration and permutation of an input (such as an image) to understand all input cases. To avoid having to augment the data a multitude of times, one could leverage the geometry of the image. Leveraging the geometry of the task at hand is not a novel concept -- in the field of image analysis, when considering a 2-D image, convolutional neural networks (CNNs) are able to detect an object irrespective of its position within the image. By respecting the geometry of the task at hand, the model learns more efficiently, as one can significantly reduce the number of trainable parameters [22].

In machine learning, the notion of symmetry is often recast in terms of invariance and equivariance. These express the behaviour of any mathematical function with respect to a transformation $T$ of an acting symmetry group [23]. Based on the definitions provided in [17], we illustrate these concepts below. We take a mathematical function, $F$, which we apply to a given input, $X$. $F(X)$ can therein transform equivariantly or invariantly:

• Equivariance: A function $F$  applied to an input $X$ is equivariant to a transformation $T$ if the transformation of  $X$ commutes with the transformation of $F(X)$, via a transformation $T$  of the same symmetry group, such that: $F(T(X)) = T(F(X))$.
• Invariance: Invariance is a special case of equivariance, where $F(X)$ is invariant to $T$ if $T$ is the trivial group action (i.e., identity): $F(T(X)) = T(F(X)) = F(X)$.

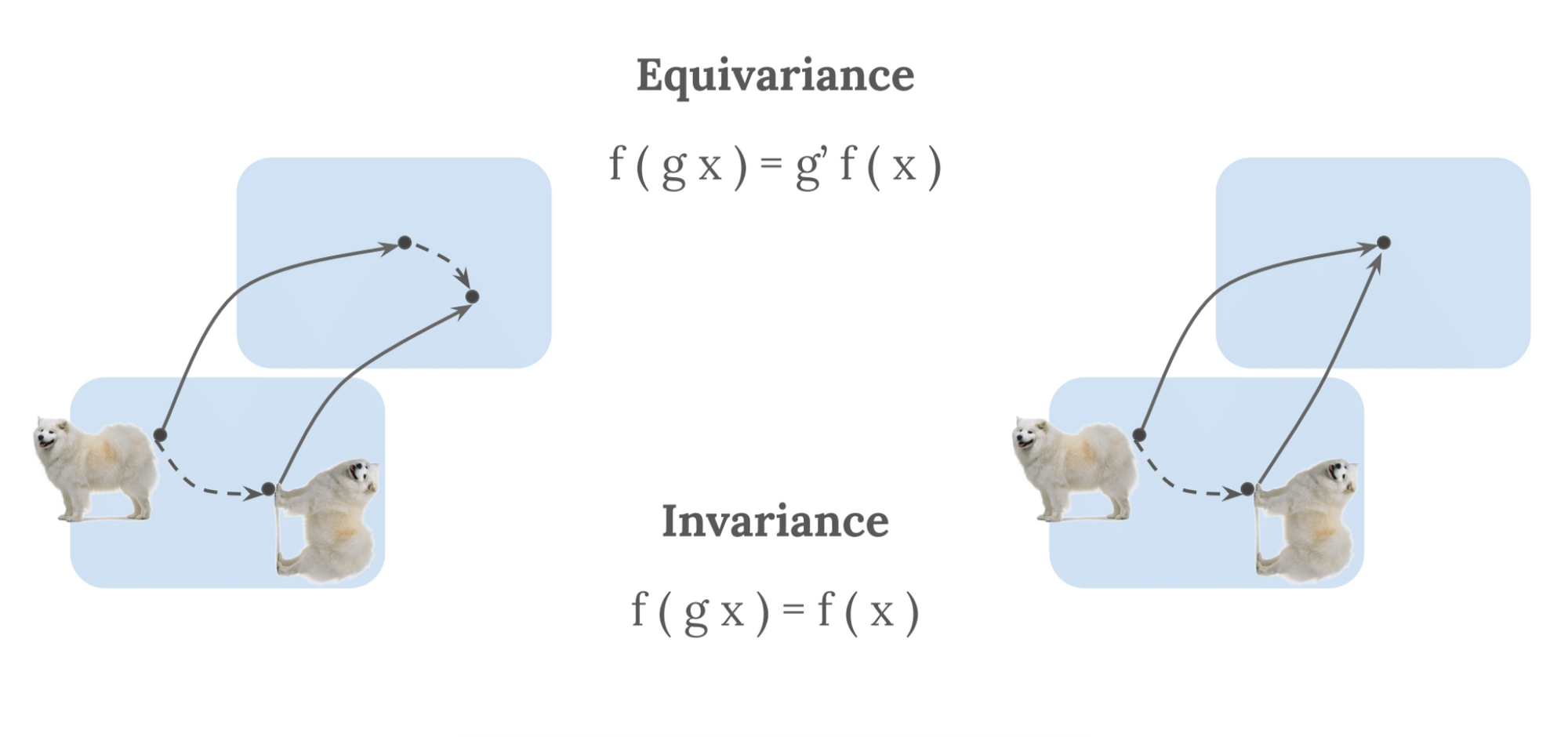
Or, in other words, equivariance deals with the notion that one transforms the output in the same way one transforms the input, while invariance deals with the notion that transformations of the input do not affect the output, as visible in Figure 3.

For molecules, relevant transformations within the 3D space involve rotations, and translations are part of a symmetry group under which a system is invariant. This symmetry group is denoted as the special Euclidean group in 3 dimensions, SE(3). The difference between the Euclidean group in 3 dimensions, E(3), is the omission of the reflection as a valid transformation. This principle introduces us to the notion of translation invariance: for a molecule of  atoms, translating our input coordinates $r_1, \dots, r_n$ by $g \in R_3$  to become $r_{1} +g, \dots, r_{n} +g$, which should not change the output of the model [20].

However, this is not entirely true for chiral molecules, as transforming the molecular representation does change the molecule. Their biological and pharmacological properties can significantly change depending on the handedness of the molecule. This is exemplified by enantiomers, which are pairs of molecules that are mirror images of each other, but have different pharmacological properties [25].

Enantiomers can have very different effects -- mirroring an enantiomer could either yield a lead candidate or a deadly toxin [26]. With this in mind, it would be desirable to consider machine learning systems that take into account the symmetry of the task at hand. Thus, integrating symmetry into these modelling tasks has recently been considered a valuable addition to the model to represent these systems and interactions more faithfully. Some recent papers have leveraged this technique within the field of molecular design, of which two will be briefly explained below.

E(n) Equivariant Normalizing Flows  

To understand the functioning of the normalizing flow, we first start by considering the class of generative models. Under the umbrella term of generative models, we consider (1) energy-based models, (2) variational autoencoders, (3) generative adversarial networks, (4) normalizing flows, and (5) diffusion models.

Mathematically defined, generative models typically consist of two elements, which are a distribution $p_z$ and a learnable function $g: z \rightarrow x$, where $z$ denotes the latent space and $x$ denotes an arbitrary point in the sample space. Discriminative models, on the other hand, have a learnable function of the form $g: x \rightarrow y$, where $x$ denotes an arbitrary point in the sample space, and $y$ denotes the labels of the learned features in the feature space. The difference lies in how $g$ is learned, i.e. what the objective function is. Generative models aim to model the training distribution in order to sample new data points, whilst discriminative models aim to model the decision boundary between classes.

While the aforementioned generative models all share distinct objectives, they may not necessarily learn the exact probability density function $p(x)$ and likelihood, which are both difficult to compute. This is where the class of normalizing flows come in. The likelihood of a point $x$ can be found by inverting the learnable function $g^{-1}$ and going back to a point in the latent space $z$, which is done through a slight change in the variables. Applying normalizing flows to molecular instances, in this case, generating molecular features and 3-D positions, would require the positional information of nodes $x \in R^{M\times n}$, where $M$ denotes the number of nodes present in the $n$-dimensional space. An atom type is represented by $h$, where $h$ is the representation in $R^{M \times nf}$. The discrete features $h$ are mapped into a continuous latent space, yielding the following for the change of variables formula [27,28].

The learnable function $f$ is constructed by the development of a Neural Ordinary Differential Equation (NODE) of which the dynamics are governed by an E(n) Equivariant Graph Neural Network (E-GNN) [29]. In differential equations, we would simply aim to find the derivative of a function. However, ordinary differential equations use the concept of evolution of the derivative that slowly converges towards an analytical estimate of the solution. Integrating the NODE collects all the terms for the likelihood, among which lies the base distribution on the output $\log P_z(z_x, z_h)$ [28]. Taken all together, this would yield the following procedure:

It was found that the E-NF significantly outperformed non-equivariant models in terms of log-likelihood and that it produced 85% valid atom configurations based on 10.000 generated examples. Using the method, 4.91% were stable, and of this subset, 99.80% were unique and 93.28% were novel.

E(3) Equivariant Diffusion Models

A more recent method is the use of E(3) Equivariant Diffusion Models for molecule generation [30,31]. Diffusion models fall under the same class of generative models, which have been described above. However, the sampling procedure differs. Let us recall that we have the positional information $x$ of the nodes and $h$ denoting the different atom types. A forward diffusion process is defined by adding a small amount of Gaussian noise to the sample in $T$, producing a sequence of noisy samples $x_1, \dots, x_t$, with a controlled step size [32]. In other words, diffusion models are trained to reverse this noising process. In order to generate new samples at inference time, one starts with a Gaussian distribution and uses the trained diffusion model to remove noise stepwise until one arrives at a "final" sample. Comparing this approach to the previous method, it was found that it significantly outperforms state-of-the-art generative methods in terms of the scalability, quality, and efficiency of the network. Bringing this together yields the following procedure:

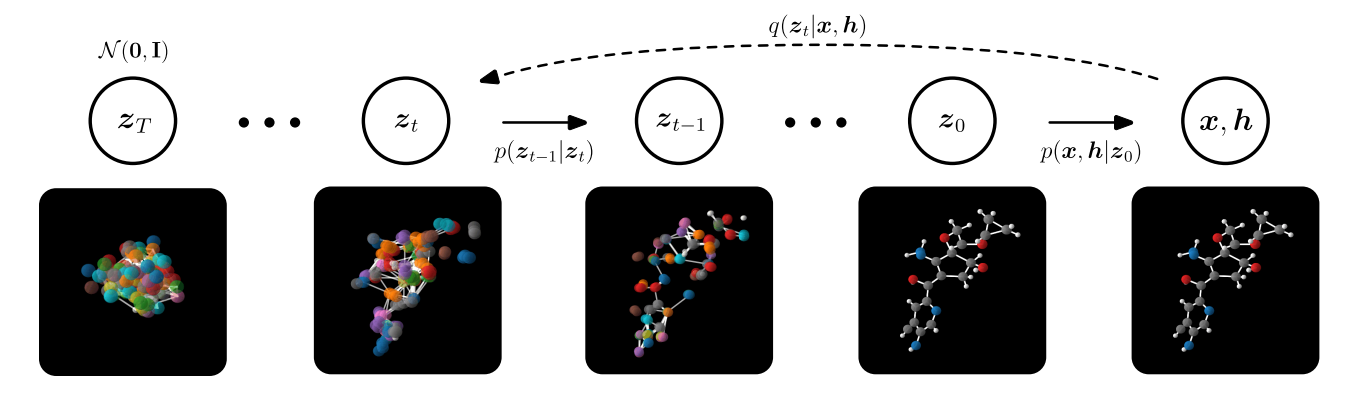
In comparison to the E-NF, EDMs are able to generate 16x more stable molecules than E-NF, while only using half of the training time, which significantly increases the amount of (novel) compounds available. The more stable and testable compounds there are, the higher the probability of finding a novel candidate in the high-throughput screening phase that might work. However, what is important to note is that stability is a trivial metric for in silico design as all drug molecules must be stable. Nonetheless, a more relevant metric would be synthesizability (which refers to the steps needed to synthesise the molecule) because many stable, generated molecules are nowhere near synthesizable [33].

However, if we put the presented numbers from both studies in perspective -- typical success rates (so-called “hit-rates”, which showcase the most optimal molecule based on their bioactivity) from human-based experimental methods are in the range of 0.01-0.14%, while virtual screen rates are between 1-40% [34], showing a significant increase in finding the best compounds. It must be noted that the experiments described in both of the studies are done on datasets with a small number of samples.

At the scale of real-world applications, integrating the full geometric information would require an incredible amount of computational resources. Alternatives have been proposed, for example in [20], which provides a novel approach to implicitly integrating the 3D geometry of molecules into the neural network’s learning process, while only requiring 2D molecular graphs when using the network to make predictions. While using more detailed representations (i.e. 2D -> 3D -> beyond) is a step in the right direction, the availability of data drastically drops. The real-world performance of these models is bottlenecked by the availability of high-quality geometric data (unlike the benchmark datasets in academic papers). To make further progress, we need to start thinking about data generation. Even though the recent methods have demonstrated their success in small-scale case studies, and there might be more on the horizon -- this might just be a glimpse of the undiscovered iceberg of future drug candidates.

A New Era of Scientific Discovery?

We have seen how machine learning can accelerate the process of traditional drug discovery, and it is undeniable that it will act as a strong catalyst for future research.

Using computer-aided methods for drug discovery significantly reduces the monetary and human resources spent on the screening procedure, as they can find suitable lead candidates faster, and devote less time to synthesising non-promising compounds. This aids us in our understanding of how drug candidates work, as these models add an extra layer to the preclinical drug discovery funnel. This brings us to the prospect of lowering costs for drug development, with the eventual grand objective to develop drugs for rare diseases. This paradigm shift can potentially complement our current biological and chemical understanding of the natural and physical sciences.

The recent advances in AI have great potential to reinvent the status quo and rethink and accelerate how we tackle the many global, societal challenges we face. It is undeniable that their influence will only increase in the coming years. With the advent of Moore’s Law in 1965, which has been considered a driving force of technological innovation and social change, this is not going to change anytime soon. What was unimaginable generations ago becomes imaginable. Molecules are vital to life as we know it. They carry information to our cells from other cells, our food, the air we breathe, and the drugs we take. Their complexity means that they are both fundamental to biology whilst still being poorly understood. However, advances in our understanding of the physicochemical properties of molecules and how these properties interact with cells are expected to usher in a new era of drug discovery. It is very possible that the era has just begun.

Author Bio

Meilina Reksoprodjo is an MSc student in Data Science in Engineering at the Eindhoven University of Technology (TU/e), specializing in explainable AI & geometric deep learning in the context of drug discovery. She holds a BSc degree in Artificial Intelligence from Radboud University. For more updates, she is active on Twitter or Linkedin.

Acknowledgements

The author is grateful to Marco Cognetta, David D, Lin Min Htoo, Koen Minartz, Rıza Ozcelik, Tadija Radusinović, Maxim Snoep, Dr. Namid Stillman, Esther Shi, Koen Smeets, Sang Truong, Joost van der Haar, Stefan van der Sman, Derek van Tilborg and Dr. Yew Mun Yip for proofreading this article and providing valuable input for improving the text.

Citation

For attribution in academic contexts or books, please cite this work as

Meilina Reksoprodjo, "Symmetries, Scaffolds, and a New Era of Scientific Discovery", The Gradient, 2022.

BibTeX citation:

@article{reksoprodjooverview2022,
author = {Meilina Reksoprodjo},
title = {Symmetries, Scaffolds, and a New Era of Scientific Discovery},
journal = {The Gradient},
year = {2022},
howpublished = {\url{https://thegradient.pub/symmetries-scaffolds-and-a-new-era-of-scientific-discovery} },
}

Bibliography

[1] D. Sun, W. Gao, H. Hu and S. Zhou, "Why 90% of clinical drug development fails and how to improve it?", Acta Pharmaceutica Sinica B, vol. 12, no. 7, pp. 3049-3062, 2022. Available: 10.1016/j.apsb.2022.02.002.

[2] A. Mullard, "Parsing clinical success rates", Nature Reviews Drug Discovery, vol. 15, no. 7, pp. 447-447, 2016. Available: 10.1038/nrd.2016.136.

[3] R. Gómez-Bombarelli et al., "Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules", ACS Central Science, vol. 4, no. 2, pp. 268-276, 2018. Available: 10.1021/acscentsci.7b00572.

[4] J. Kim and A. Scialli, "Thalidomide: The Tragedy of Birth Defects and the Effective Treatment of Disease", Toxicological Sciences, vol. 122, no. 1, pp. 1-6, 2011. Available: 10.1093/toxsci/kfr088.

[5] C. Yerkes, "Lecture 22", Butane.chem.uiuc.edu, 2022. [Online]. Available: http://butane.chem.uiuc.edu:80/cyerkes/Chem204sp06/Lecture_Notes/lect21c.html.

[6] M. M. Bronstein, J. Bruna, T. Cohen, and P. Velickovič, “Geometric deep learning: Grids, groups, graphs, geodesics, and gauges”, arXiv:2104.13478, 2021.

[7] J. Vamathevan et al., "Applications of machine learning in drug discovery and development", Nature Reviews Drug Discovery, vol. 18, no. 6, pp. 463-477, 2019. Available: 10.1038/s41573-019-0024-5.

[8] G. Sliwoski, S. Kothiwale, J. Meiler and E. Lowe, "Computational Methods in Drug Discovery", Pharmacological Reviews, vol. 66, no. 1, pp. 334-395, 2013. Available: 10.1124/pr.112.007336.

[9] S. Kim et al., "PubChem Substance and Compound databases", Nucleic Acids Research, vol. 44, no. 1, pp. D1202-D1213, 2015. Available: 10.1093/nar/gkv951.

[10] G. Papadatos, A. Gaulton, A. Hersey and J. Overington, "Activity, assay and target data curation and quality in the ChEMBL database", Journal of Computer-Aided Molecular Design, vol. 29, no. 9, pp. 885-896, 2015. Available: 10.1007/s10822-015-9860-5.

[11] J. Howard, "The business impact of deep learning", Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, 2013. Available: 10.1145/2487575.2491127.

[12] B. McMahon, "AI is Ushering In a New Scientific Revolution", The Gradient, 2022. Available: https://thegradient.pub/ai-scientific-revolution/

[13] H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, "The rise of deep learning in drug discovery", Drug Discovery Today, vol. 23, no. 6, pp. 1241-1250, 2018. Available: 10.1016/j.drudis.2018.01.039.

[14] K. Roy, S. Kar and R. Das, A primer on QSAR/QSPR modeling, 1st ed. Springer, 2015, pp. 1-36.

[15] Z. Wu et al., "MoleculeNet: a benchmark for molecular machine learning", Chemical Science, vol. 9, no. 2, pp. 513-530, 2018. Available: 10.1039/c7sc02664a.

[16] D. Weininger, "SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules", Journal of Chemical Information and Modeling, vol. 28, no. 1, pp. 31-36, 1988. Available: 10.1021/ci00057a005.

[17] K. Atz, F. Grisoni and G. Schneider, "Geometric deep learning on molecular representations", Nature Machine Intelligence, vol. 3, no. 12, pp. 1023-1032, 2021. Available: 10.1038/s42256-021-00418-8.

[18] E. Jannik Bjerrum, R. Threlfall. “Molecular Generation with Recurrent Neural Networks (RNNs)”.  arXiv:1705.04612, 2017.

[19] Y. Rong et al., "Self-Supervised Graph Transformer on Large-Scale Molecular Data", Proceedings of the 33th International Conference on Neural Information Processing Systems (NeurIPS), 2020, pp. 12559–12571.

[20] H. Stark et al., “3-D Infomax improves GNNs for Molecular Property Prediction”, presented at the 39th International Conference on Machine Learning (ICML), 2022.

[21] T. Smidt, "Euclidean Symmetry and Equivariance in Machine Learning", Trends in Chemistry, vol. 3, no. 2, pp. 82-85, 2021. Available: 10.1016/j.trechm.2020.10.006.

[22] A. White, "Deep learning for molecules and materials", Living Journal of Computational Molecular Science, vol. 3, no. 1, 2022. Available: 10.33011/livecoms.3.1.1499.

[23] J. Marsden and A. Weinstein, "Reduction of symplectic manifolds with symmetry", Reports on Mathematical Physics, vol. 5, no. 1, pp. 121-130, 1974. Available: 10.1016/0034-4877(74)90021-4.

[24] E. van der Pol, "AMMI Seminar 1 - Geometric Deep Learning and Reinforcement Learning", African Masters of Machine Intelligence [Online], 2021.

[25] L. Nguyen, H. He and C. Pham-Huy, "Chiral Drugs: An Overview", International Journal of Biomedical Science, vol. 2, no. 2, pp. 85-100, 2006.

[26] W. H. Brooks, W. C. Guida and K. G. Daniel, "The Significance of Chirality in Drug Design and Development", Current Topics in Medicinal Chemistry, vol. 11, no. 7, pp. 760-770, 2011. Available: 10.2174/156802611795165098.

[27] V. G. Satorras, E. Hoogeboom, F. B. Fuchs, I. Posner, and M. Welling. “E(n) equivariant Normalizing Flows”, in the 34th Advances in Neural Information Processing Systems (NeurIPS) [Online], 2021. Available: https://proceedings.neurips.cc/paper/2021/hash/21b5680d80f75a616096f2e791affac6-Abstract.html

[28] E. Hoogeboom, "How to build E(n) Equivariant Normalizing Flows, for points with features?", ehoogeboom.github.io/, 2022. [Online]. Available: https://ehoogeboom.github.io/post/en_flows/.

[29] V. G. Satorras, E. Hoogeboom, and M. Welling. “E(n) equivariant graph neural networks”, in Proceedings of the 38th International Conference on Machine Learning (ICML) [Online], 2021. Available: http://proceedings.mlr.press/v139/satorras21a/satorras21a.pdf.

[30] E. Hoogeboom et al., “Equivariant Diffusion for Molecule Generation in 3-D”, in Proceedings of the 39th International Conference on Machine Learning,(ICML), 2022, pp. 8867--8887.

[31] M. Xu, L. Yu, Y. Song, C. Shi, S. Ermon and J. Tang, "GeoDiff: A Geometric Diffusion Model for Molecular Conformation Generation", presented at the 11th International Conference on Learning Representations (ICLR 2022) [Online]. Available: arXiv:2203.02923.

[32] L. Weng, "What are Diffusion Models?", lilianweng.github.io, 2022. [Online]. Available: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/.

[33] W. Gao and C. Coley, "The Synthesizability of Molecules Proposed by Generative Models", Journal of Chemical Information and Modeling, vol. 60, no. 12, pp. 5714-5723, 2020. Available: 10.1021/acs.jcim.0c00174.

[34] T. Zhu et al., "Hit Identification and Optimization in Virtual Screening: Practical Recommendations Based on a Critical Literature Analysis", Journal of Medicinal Chemistry, vol. 56, no. 17, pp. 6560-6572, 2013. Available: 10.1021/jm301916b.